Home >> PURE MATHS, Differential Calculus, exponentials, logarithms

Exponential Functions

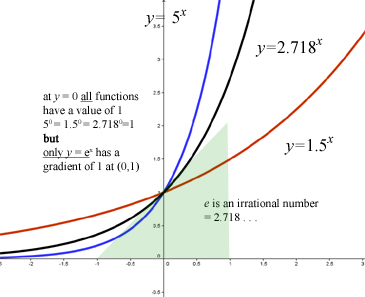
Strictly speaking all functions where the variable is in the index are called exponentials.

The Exponential function e ^x

This is the one particular exponential function where 'e' is approximately 2.71828 and the gradient of y = e ^x at (0,1) is 1.

One other special quality of y = e ^x is that its derivative is also equal to e ^x,

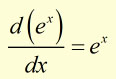
and for problems of the type y = e ^kx :

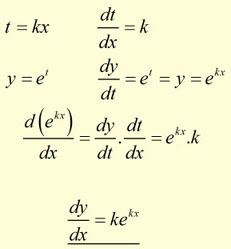
Derivative problems like the above concerning 'e' are commonly solved using the Chain Rule.

Example #1

Find the derivative of:

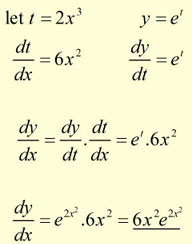
Example #2

Find the derivative of:

back to top

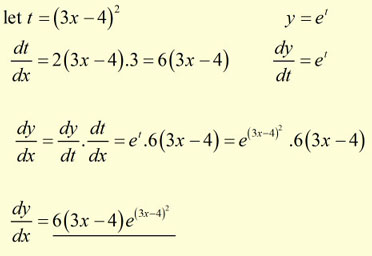
Derivative of a Natural Logarithm Function

Remember y = log _e x means:

x is the number produced when e is raised to the power of y

The connection between y = e ^x and y = log _e x can be shown by rearranging y = log _e x.

y = log _e x   can be written as   x = e ^y

(log _e x is now more commonly written as ln(x) )

The derivative of ln(x) is given by:

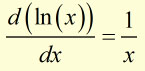
Example #1

Find the derivative of y = ln(3x).

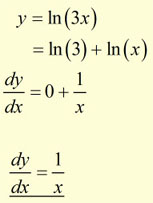
Example #2

Find the derivative of y = ln(x³+3).

back to top

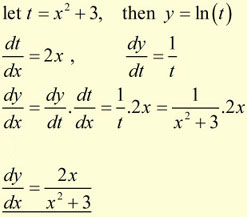
Problems of the type y = N ^f(x)

Problems of this type are solved by taking logs on both sides and/or using the Chain Rule.

Example #1

Find the derivative of y = 10 ^x.

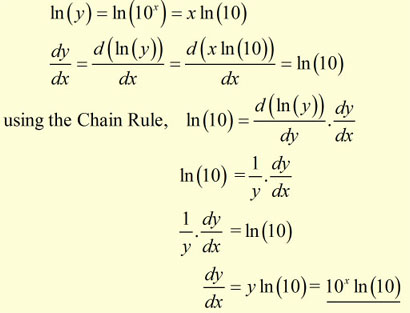
Example #2

Find the derivative of y = ln(cos³2x).

back to top

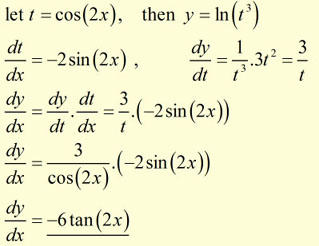
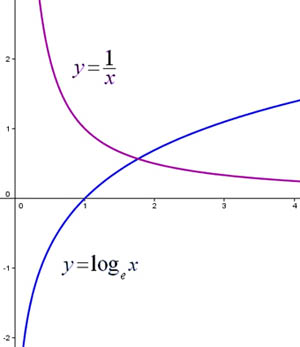
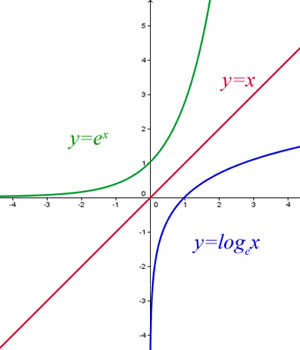
A Graphical Comparison of Exponential and Log Functions

As you can see, y = e ^x is reflected in the line y = x to produce the curve y = ln(x).

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]