Home >> PURE MATHS, Sequences & Series, sigma notation

Introduction

An ordered set of numbers obeying a simple rule is called a sequence.

A series or progression is when the terms of a sequence are considered as a sum.

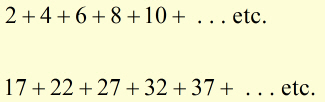
Sigma Notation

Instead of writing long expressions like:

where n is the 'last term'.

We are able to write:

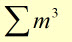
which means ' the sum of all terms like m³ ' .

To show where a series begins and ends, numbers are placed above and below the sigma symbol. These are equal to the value of the variable, 'm' in this case, taken in order.

Hence,

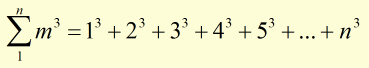
more examples,

back to top

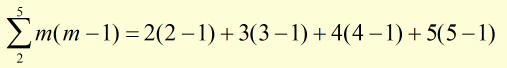
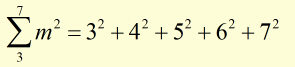
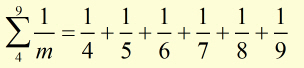
Convergence

This concerns geometrical progressions that as the number of terms increase, the value of the sum approaches one specific number. This number is called the sum to infinity.

Look at this example.

As the number of terms(n) increases, the sum of the progression( S_n ) approaches 2 .

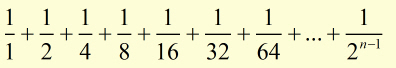
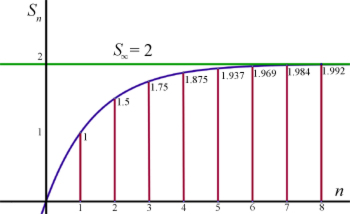
You can find out more about convergent series in the topic geometrical progressions.

back to top

Recurrence

Recurrence is when there is some mathematical relation between consecutive terms in a sequence.

The Fibonacci Sequence is a good example of this.

The numbers of the sequence are made up by adding the two previous numbers.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]