Home >>STATISTICS, Section 2, binomial distribution 4

Cumulative Probability Tables - case of p>0.5

These give the tabulated value of P(X< x) . This means that the probability displayed is less than or equal to an observed value of x.

The random variable X is distributed Binomially, where there are n trials and probability of success p .

Working out values of random variable probabilty P(X) for the case of p>0.5 is complicated by the fact that values of p only go up to 0.5 .

The way around this problem is to consider another random variable Y , representing failure.

So we have:

p_X + p_Y = 1

In the same way as X, Y is distributed binomially:

Y ~ B(n,1 - p_Y)

Say that the random variable X has values X = 0, 1, 2, 3, 4, 5

A table of values for X (success) and Y (failure) looks like this:

The method is to use the table to produce an expression in Y that will use values of p<0.5 .

back to top

The case      P(X<x)

Say we wish to find the value of P(X<4) for :

X = 0, 1, 2, 3, 4, 5      p_X=0.85*       n=6

tables only go up to 0.5

X (success) and Y (failure) are related so:

The sum of successes and failures for each outcome must always be the same (ie 5).

The probability for Y becomes p_y=0.15*     (p_X + p_Y= 1)

* p_y <0.5 and therefore on the table

From the table,

P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4)

= P(Y=5) + P(Y=4) + P(Y=3) + P(Y=2) + P(Y=1)

this can be written:

P(X<4) = P(Y>1)

since,

P(Y=0) + P(Y=1) + P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5) = 1

P(Y=1) + P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5) = 1 - P(Y=0)

in other words,

P(Y>1) = 1 - P(Y<0)

hence the original inequality can be rewritten :

P(X<4) = 1 - P(Y<0)

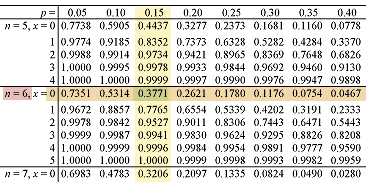
Using the tables to find the value of P(Y<0) for n=6 p_Y=0.15 , Y=0 :

P(Y<0) = 0.3771

hence,

P(X<4) = 1 - 0.3771 = 0.6229

back to top

The case      P(X=x)

Consider the binomial distribution for success,

X ~ B(n, p_X)

X = 0, 1, 2, 3, 4, 5      p_X=0.85       n=6

also the binomial distribution for failure,

Y ~ B(n, p_Y)

Y= 0, 1, 2, 3, 4, 5      p_Y=0.15       n=6

Say we want to find P(X=4).

From the table it follows that,

P(X=4) = P(Y=1)

P(Y=1) = P(Y<1) - P(Y<0)

P(X=4) = P(Y<1) - P(Y<0)

P(X=4) = 0.7765 - 0.3771 = 0.3994

back to top

The case     P(X<x)

Consider the binomial distribution for success,

X ~ B(n, p_X)

X = 0, 1, 2, 3, 4, 5      p_X=0.85       n=6

also the binomial distribution for failure,

Y ~ B(n, p_Y)

Y= 0, 1, 2, 3, 4, 5      p_Y=0.15       n=6

Say we want to find P(X<4).

From the table it follows that,

P(X<4) = P(Y>1)

and

P(Y>1) = P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5)

it follows that,

P(Y>1) = P(Y>2)

P(Y>2) = P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5)

P(Y=0) + P(Y=1) + P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5) = 1

P(Y=2) + P(Y=3) + P(Y=4) + P(Y=5) = 1 - [ P(Y=0) + P(Y=1)]

P(Y>2) = 1 - [ P(Y=0) + P(Y=1)]

P(Y>2) = 1 - P(Y<1)

P(X<4) = 1 - P(Y<1)

P(X<4) = 1 - 0.7765 = 0.2235

back to top

The case     P(X>x)

Consider the binomial distribution for success,

X ~ B(n, p_X)

X = 0, 1, 2, 3, 4, 5      p_X=0.85       n=6

also the binomial distribution for failure,

Y ~ B(n, p_Y)

Y = 0, 1, 2, 3, 4, 5      p_Y=0.15       n=6

Say we want to find P(X>4).

P(X>4) = P(Y<1)

P(Y<1) = P(Y=0)

P(Y=0) = P(Y<0)

P(X>4) = P(Y<0)

reading P(Y<0) directly from the tables,

P(X>4) = 0.3771

back to top

The case     P(X>x)

Consider the binomial distribution for success,

X ~ B(n, p_X)

X = 0, 1, 2, 3, 4, 5      p_X=0.85       n=6

also the binomial distribution for failure,

Y ~ B(n, p_Y)

Y = 0, 1, 2, 3, 4, 5      p_Y=0.15       n=6

Say we want to find P(X>4).

P(X>4) = P(Y<1)

reading P(Y<1) directly from the tables,

P(X>4) = 0.7765

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]