Home >> PURE MATHS, Algebra, iteration

Introduction

Repeatedly solving an equation to obtain a result using the result from the previous calculation, is called 'iteration'.

The procedure is used in mathematics to give a more accurate answer when the original data is only approximate.

Problems usually involve finding the root of an equation when only an approximate value is given for where the curve crosses an axis.

Direct/Fixed Point Iteration

method:

1. Rearrange the given equation to make the highest power of x the subject.

2. Find the power root of each side, leaving x on its own on the left.

3. The LHS x becomes   x_n+1 .

4. The RHS x becomes   x_n .

The equation is now in its iterative form.

We start by working out x₂ from the given value x₁ .

x₃ is worked out using the value x₂ in the equation.

x₄ is worked out using the value x₃ and so on.

Example

Find correct to 3 d.p. a root of the equation:

f(x) = x³ - 2x + 3

Given that there is a solution near   x = -2

back to top

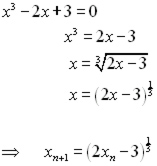
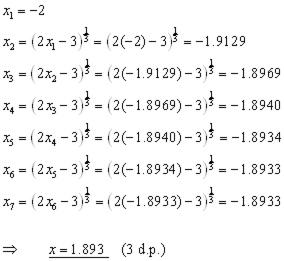
Iteration by Bisection

method:

1. Reduce the interval where the root lies into two equal parts.

2. Decide in which part the solution resides.

3. Repeat the process until a consistent answer is achieved for the degree of accuracy required.

Example

Find correct to 3 d.p. a root of the equation:

f(x) = 2x²- 2x + 7

given that there is a solution near   x = -2 .

back to top

Newton-Raphson Method

This uses a tangent to a curve near one of its roots and the fact that where the tangent meets the x-axis gives an approximation to the root.

The iterative formula used is:

Example

Find correct to 3 d.p. a root of the equation:

f(x) = 2x² + x - 6

given that there is a solution near   x = 1.4 .

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]