Home >> PURE MATHS, Integration, volumes of revolution

Method

A volume(rotated around the x-axis)is calculated by first considering a particular value of a function, y₁, up from a value of x at x₁ .

The line x₁y₁ may be considered as the 'radius' of the solid at that particular value of x.

If you were to square the y-value and multiply it by pi, then a cross-sectional area would be created.

Making a solid of revolution is simply the method of summing all the cross-sectional areas along the x-axis between two values of x.

(compare: area of a cylinder = cross-sectional area x length)

The method for solids rotated around the y-axis is similar.

Rotation around the x-axis

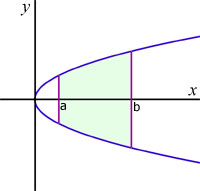
The volume V_xof a curve y=f(x) rotated around the x-axis between the values of x of a and b, is given by:

Example

What is the volume V of the cone swept out by the line y=2x rotated about the x-axis between x=0 and x=5 ?

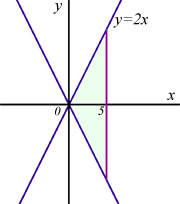
using   

and substituting                                  

      therefore              

back to top

Rotation around the y-axis

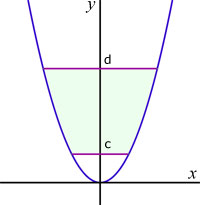
The volume V_yof a curve y=f(x) rotated around the x-axis between the values of y of c and d, is given by:

Example

What is the volume V of the 'frustrum'(cone with smaller cone-shape removed) produced when the line y=2x/3 is rotated around the y-axis, when the centres of the upper and lower areas of the frustrum are at 0,7 and 0,3 ?

back to top

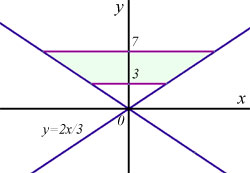
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]