Home >>STATISTICS, Section 1, discrete random variables 1

Concept

The basic idea is assign a real number x_r to every event E_r happening in the sample space S .

Example

Consider the case when a coin is tossed twice. The possible results( the Sample Space S) are:

(T T)   (T H)   (H T)   (H H)

Assigning numbers for the number of 'heads' (H) occuring:

(0)   (1)   (1)   (2)

So overall, there are 3 possible outcomes:

no heads     one head     two heads

This can be written as the result:

0               1              2

So the probability of flipping a coin twice and obtaining a head is given by:

back to top

The Probability (Density) Function PDF

The probability function of X, written as P(X=x), is used to allocate probabilities.

We describe X as a discrete random variable, when it has a finite number of possible values and if the sum of probabilities is one.

X takes the value x_r when the event E_r occurs.

From our example(above) it is self evident that:

   event E = 1     one head    x = 1      P(X=1) = 1/2

So all the results in our example could be displayed as:

The probability function can also be written as p(x) .

therefore,

P(X=x) = p(x)

back to top

Cumulative Distribution Function CDF

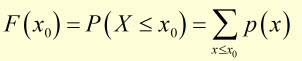
This function returns the sum of probabilities of X for values of x less than or equal to x₀ .

It also may be described as the function F(x₀) giving the probability of X when its value is less than or equal to x₀ .

A more general definition is that cumulative probability F(x₀) is the value a random variable takes when it falls between a specific range.

Example #1

Consider a situation where there are four possible outcomes(x = 0, 1, 2, 3 ), with different probabilities for each of these.

The probability that X is less than or equal to 3 is given by:

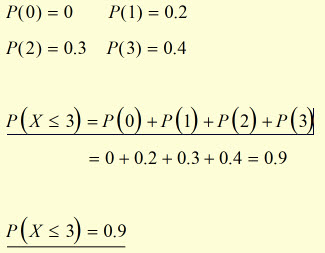
Example #2 (with reference to the coin flip table above)

A coin is flipped twice. What is the probability that '1' head or '0' heads result?

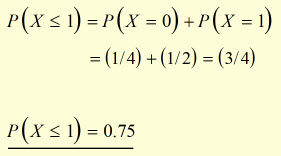
All the results for heads(x) from 2 coin flips can be summarized in a modified table:

Notice how P(X<x) is derived from P(X=x) when x is incremented.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]