Home >> PURE MATHS, Trigonometry, sine, cosine, tangent

The General Angle

Consider a radius of length '1' rotating anti-clockwise about the origin.

The coordinates of any point on the circle give the values of the adjacent and opposite sides of a right angled triangle, with the radius the hypotenuse.

The General Angle ( θ theta) is the included angle between the radius and the x-coordinate of the point.

As the radius rotates the x and y values change. Hence the values of sine, cosine and tangent also change.

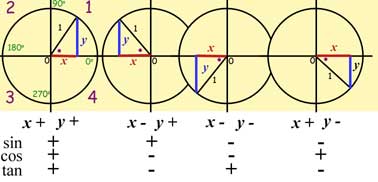
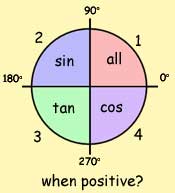
The result is summarized in the diagram below.

Example #1

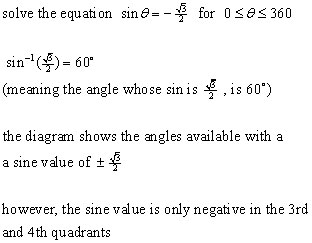
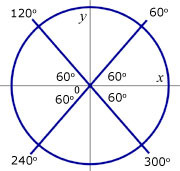
Example #2

back to top

Sine

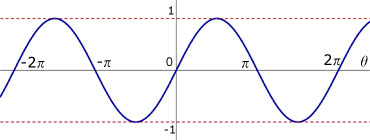
Points of interest :

The 'sine graph' starts at zero.

It repeats itself every 360 degrees(or 2 pi).

y is never more than 1 or less than -1

(vertical displacement from the x-axis is called the amplitude).

A 'sin graph' leads a cos graph by 90 degrees

back to top

Cosine

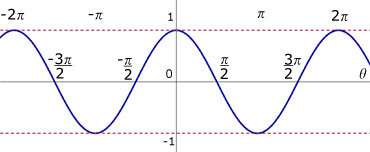
Points of interest:

The 'cosine graph' starts at one.

It repeats itself every 360 degrees(or 2 pi).

y is never more than 1 or less than -1

(displacement from the x-axis is called the amplitude).

A 'cos graph' lags a 'sin graph' by 90 degrees(pi/2) - this is termed a phase shift

back to top

Tangent

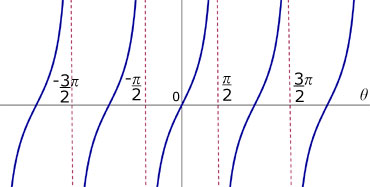
Points of interest:

The 'tangent graph' starts at zero.

It repeats itself every 180 degrees.

y can vary between numbers approaching infinity and minus infinity.

Further Comparison

Only the cosine function is symmetrical (a mirror image of itself) about the y-axis.

All the functions are cyclic - a waveform along the horizontal axis is repeated.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]