Home >> PURE MATHS, Differential Calculus, tangents & normals

Tangents

The gradient of the tangent to the curve y = f(x) at the point (x₁, y₁) on the curve is given by:

the value of dy/dx, when x = x₁ and y = y₁

back to top

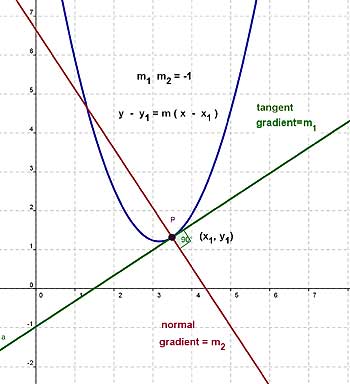
Normals

Two lines of gradients m ₁, m ₂ respectively are perpendicular to eachother if the product,

back to top

Equation of a Tangent

The equation of a tangent is found using the equation for a straight line of gradient m, passing through the point (x₁, y₁)

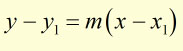
To obtain the equation we substitute in the values for x₁ and y₁ and m (dy/dx) and rearrange to make y the subject.

Example

Find the equation of the tangent to the curve y = 2x² at the point (1,2).

back to top

Equation of a Normal

The equation of a normal is found in the same way as the tangent.

The gradient(m₂) of the normal is calculated from;

(where m₁ is the gradient of the tangent)

so,

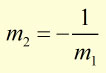
Example

Find the equation of the normal to the curve:

  y = x² + 4x + 3,   at the point (-1,0).

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]