Home >> PURE MATHS, Trigonometry, radians

What is a 'Radian'?

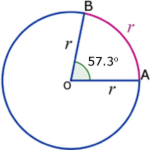
A radian is the angle subtended at the centre of a circle by an arc the same length as the radius of the circle.

Units

1^C (meaning 1 radian)= 57.296 deg.

back to top

Arc Length

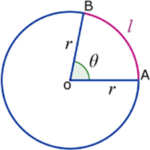
The arc length is proportional to its subtended angle.

Hence, if θ(theta) is in degrees and 'l' is the arc length:

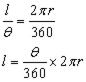
An angle can be expressed in radians by dividing the arc length by the radius.

Therefore θ in radians is given by:

Therefore for a circle(a 360 deg. angle), where the arc length is '2πr' (two pi r)and the radius is 'r' , the number of radians is 2πr/r , i.e. 2π .

back to top

Sector Area

The area of a sector is proportional to the angle its arc subtends at the centre.

If a sector contains an angle of θ^o then its area is given by:

However, if θ is in radians, remembering there are 2π radians in a circle:

back to top

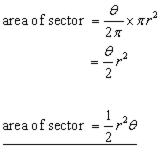
Small Angles

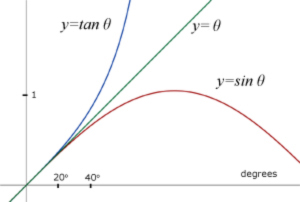
For small angles(<10 deg.) there is a convergence between the value of the angle in radians with the value of its sine & tangent.

This approximate sine value may be expressed as:

The approximate cosine value is obtained thus:

back to top

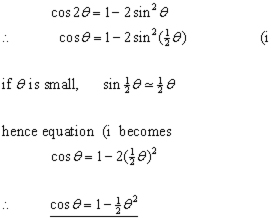
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]