Home >> PURE MATHS, Sequences & Series, geometrical series

Geometrical Series - Structure

A geometricall series starts with the first term, usually given the letter 'a'.

For each subsequent term of the series the first term is multiplied by another term.

The term is a multiple of the letter 'r' called 'the common ratio '.

So the series has the structure:

where S_nis the sum to 'n' terms, the letter 'l' is the last term.

The common ratio 'r' is calculated by dividing any term by the term before it.

The nth term(sometimes called the 'general term') is given by:

back to top

Proof of the Sum of a Geometrical Series

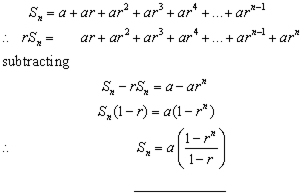
NB an alternative formula for r > 1 , just multiply numerator & denominator by -1

Example #1

In a geometrical progression the sum of the 3rd & 4th terms is 60 and the sum of the 4th & 5th terms is 120.

Find the 1st term and the common ratio.

back to top

Example #2

What is the smallest number of terms of the geometrical progression:

2 + 6 + 18 + 54 + 162 ...

that will give a total greater than 1000?

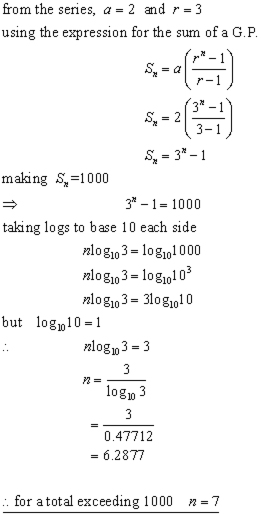
Geometic Mean

This is a method of finding a term sandwiched between two other terms.

So if we have a sequence of terms: a , b , c , where a and c are known,

the ratio of successive terms gives the common ratio.

Equating these:

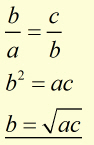
Example

If the 4th term of a geometrical progression is 40 and the 6th is 160, what is the 5th term?

back to top

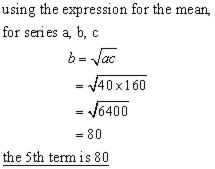
Sum to Infinity

This concerns geometrical progressions that as the number of terms increase, the value of the sum approaches one specific number. This number is called the sum to infinity.

In this example as 'n' increases the sum approaches 2 .

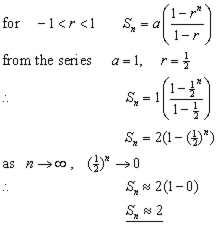
So if the term rⁿ tends to zero, with increasing n the equation for the sum to n terms changes:

Example

Express 0.055555... as a fraction.

back to top

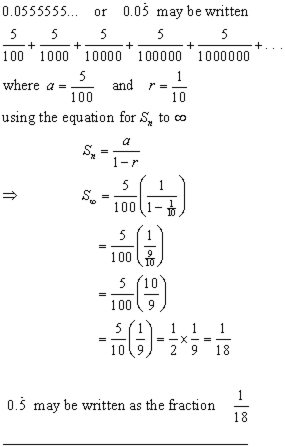
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]