Home >> MECHANICS, Kinetics, elastic strings

Hooke's Law

The extension e of an elastic string/spring is proportional to the extending force F,

where k is the constant of proportionality, called the spring constant.

By definition the spring constant is that force which will produce unit extension(unit Nm^-1) in a spring.

Example

A 2kg mass hangs at the end of an elastic string of original length 0.5 m.
If the spring constant is 60 Nm^-1, what is the length of the extended elastic string?

back to top

The energy stored in a stretched string/spring

This is the same as the work done in stretching a string.

Remembering that 'work = force x distance moved', if the elastic string is extended a small amount δe (such that the force F is considered constant), then the work done δW is given by:

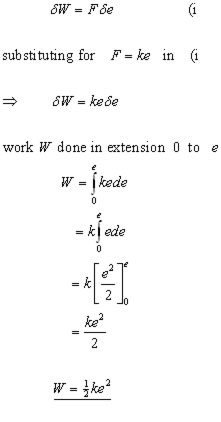
Example

A 2 kg mass m hangs at a point B at the end of an elastic string of natural length 0.7 m supported at a point A.

The extension produced in the string by the mass is a fifth of the original length, while the spring constant is 5mg.

If the mass is now held at point A and then released, what is the maximum speed the mass will attain?
(g = 10 ms^-2 , answer to 1 d.p.)

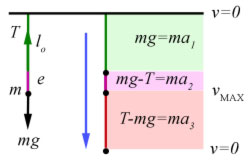
Let P.E. be related to the equilibrium position of the mass.

Hence the mass will have maximum KE when passing through point B.

Below that point there will be no net force downwards to produce acceleration.

The net force will act in the opposite direction, producing deceleration.

In the diagram,

a₁ is linear acceleration under gravity

a₂ is non-linear acceleration(decreasing)

a₃ is negative acceleration (i.e. deceleration).

back to top

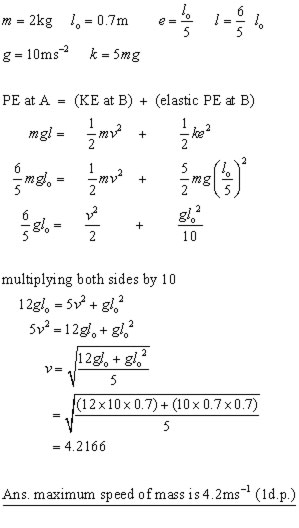
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]