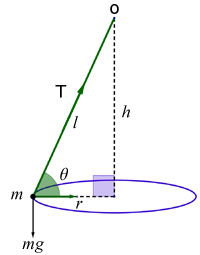
empty: coming soonConical pendulum
Problems concerning the conical pendulum assume no air resistance and that the string has no mass and cannot be stretched.
Solution of problems involves resolving forces on the mass vertically and horizontally. In this way the speed of the mass, the tension in the string and the period of revolution can be ascertained.
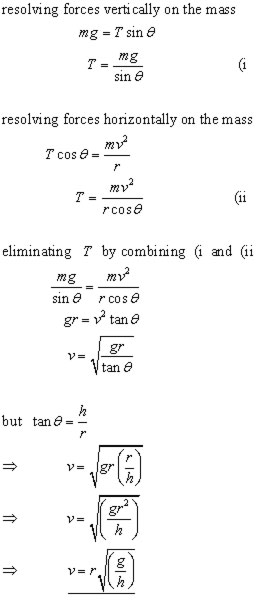
Example
A 20g mass moves as a conical pendulum with string length 8x and speed v.
if the radius of the circular motion is 5x find:
i) the string tension(assume g =10 ms-2 , ans. to 2 d.p.)
ii) v in terms of x, g
i)
ii)
Mass performing vertical circular motion under gravity
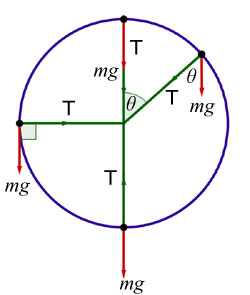
Consider a mass m performing circular motion under gravity, the circle with radius r .
The centripetal force on the mass varies at different positions on the circle.
For many problems concerning vertical circular motion, energy considerations(KE & PE) of particles at different positions are used to form a solution.
Example #1
A 50g mass suspended at the end of a light inextensible string performs vertical motion of radius 2m.
if the mass has a speed of 5 ms-1 when the string makes an angle of 30o with the vertical, what is the tension?
(assume g =10 ms-2 , answer to 1 d.p.)
Example #2
A 5kg mass performs circular motion at the end of a light inextensible string of length 3m.
If the speed of the mass is 2 ms-1 when the string is horizontal, what is its speed at the bottom of the circle?
(assume g =10 ms-2)
