Home >> PURE MATHS, Integration, area under a curve

Area Under a Curve, related to different axes

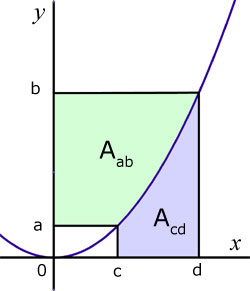
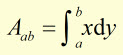
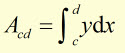
Example

Find the area 'A' enclosed by the x-axis, x = 2 , x = 4 and the graph of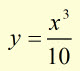

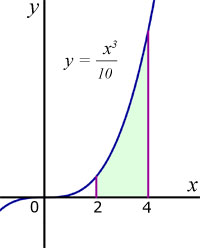
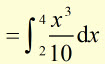
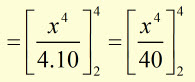
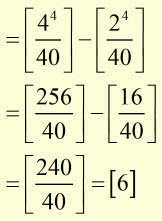
back to top

Positive and Negative Area

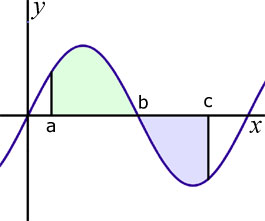
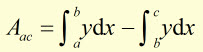
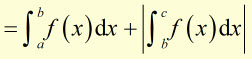
NB: This expression calculates the absolute area between the curve the vertical lines at 'a' and 'b' and the x-axis. It takes no account of sign.

If sign were an issue then the two integrals on the first line would be added and not subtracted.

Unless told differently, assume that the 'absolute area' is required.

Example

Find the area 'A' enclosed by x-axis, x = 1 , x = 8 and the graph .

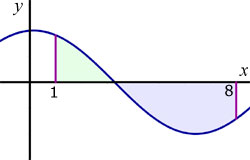
The curve crosses the x-axis at y = 0.

therefore,                                    

Sine is zero when the angle is 0, 180 or 360 deg. (ie at zero, pi and 2 pi)

back to top

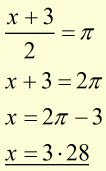
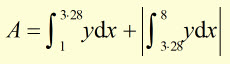
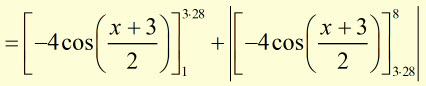
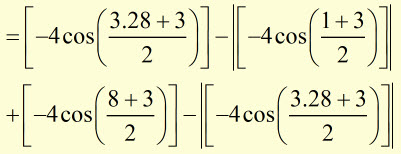
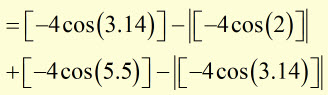
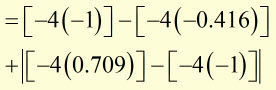
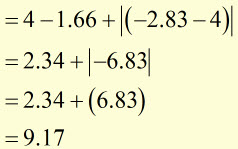
Area Bounded by Two Curves

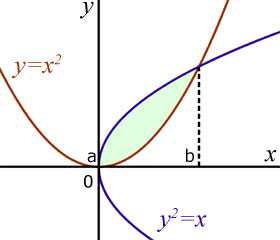
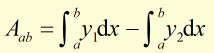
Example

To 3 d.p. calculate the area 'A' included between the curves y = x²/2 and y = (1.75)x .

First find the x-value where the curves of each function cross.

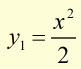
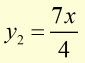
where the curves cross

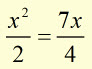
  ,     therefore 

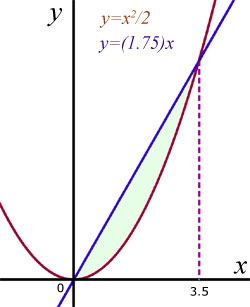
The area 'A' is the difference between the area under the straight line and the area under the parabola, from x=0 to x=3.5 .

back to top

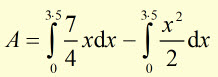
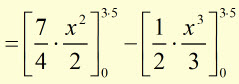
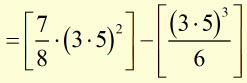
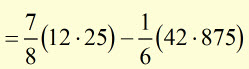
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]