Home >> MECHANICS, Linear Motion, simple harmonic motion

S.H.M. Theory

A particle is said to move with S.H.M when the acceleration of the particle about a fixed point is proportional to its displacement but opposite in direction.

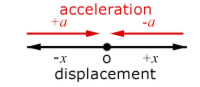
Hence, when the displacement is positive the acceleration is negative(and vice versa).

This can be described by the equation:

where x is the displacement about a fixed point O(positive to the right, negative to the left), and w² is a positive constant.

An equation for velocity is obtained using the expression for acceleration in terms of velocity and rate of change of velocity with respect to displacement(see 'non-uniform acceleration').

separating the variable and integrating,

note cos^-1() is the same as arc cos()

So the displacement against time is a cosine curve. This means that at the end of one completete cycle,

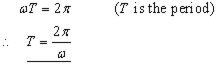
Example

A particle displaying SHM moves in a straight line between extreme positions A & B and passes through a mid-position O.

If the distance AB=10 m and the max. speed of the particle is 15 m^-1, find the period of the motion to 1 decimal place.

back to top

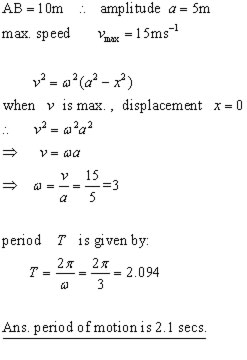
SHM and Circular Motion

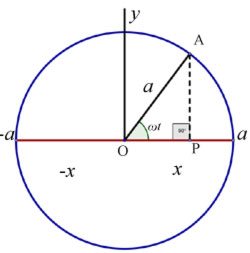
The SHM-circle connection is used to solve problems concerning the time interval between particle positions.

To prove how SHM is derived from circular motion we must first draw a circle of radius 'a'(max. displacement).

Then, the projection(x-coord.) of a particle A is made on the diameter along the x-axis. This projection, as the particle moves around the circle, is the SHM displacement about O.

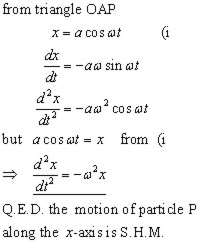
Example

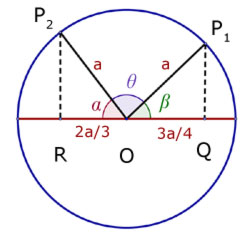
A particle P moving with SHM about a centre O, has period T and amplitude a .

Q is a point 3a/4 from O. R is a point 2a/3 from O.

What is the time interval(in terms of T) for P to move directly from Q to R?

(answer to 2 d.p.)

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]