Home >> PURE MATHS, Coordinate Geometry, straight lines ... more

Parallel Lines

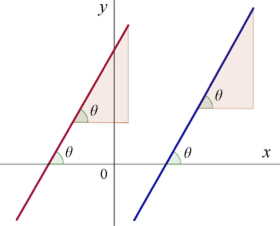
Parallel lines make equal corresponding angles(θ) with the x-axis.

Therefore their gradients are equal.

back to top

Perpendicular Lines

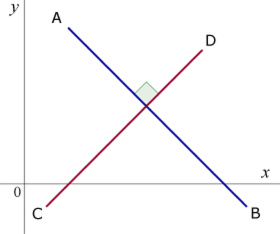
If two lines are perpendicular to eachother, the product of their gradients is -1.

If the gradient of AB is m₁ and the gradient of CD is m₂ , then:

back to top

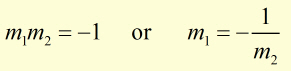
Equation of a Straight Line y = mx + c

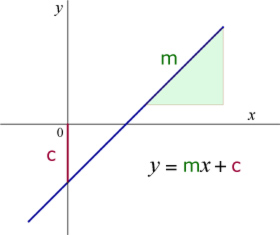
The equation of a straight line is given by:

m is the gradient of the line

c is the intercept on the y-axis

Example

What is the equation of the straight line with gradient 3 that crosses the y-axis at y= -3 ?

back to top

Finding the Intersection Point Between Two Straight Lines

There are two types of problem here.

One where the lines are not perpendicular to eachother and the other when they are.

To solve the former all that is needed is to solve the equations of the lines simultaneously.

With the later, only one equation is given and the second equation must be worked out from the information supplied. Then it is a matter of proceding as before ie to solve the two equations simultaneously.

Example #1

Find the intersection point of the two straight lines:

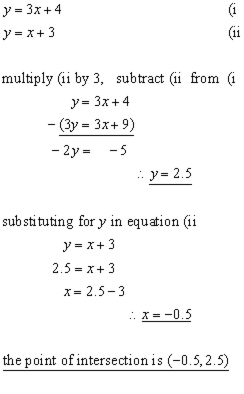
Example #2

A straight line y = 2x + 4.5 intersects another perpendicularly.

If the second straight line has an intercept of -0.5 on the y-axis, what are the coodinates of the point of intersection of the two lines? (answer to 1 d.p.)

back to top

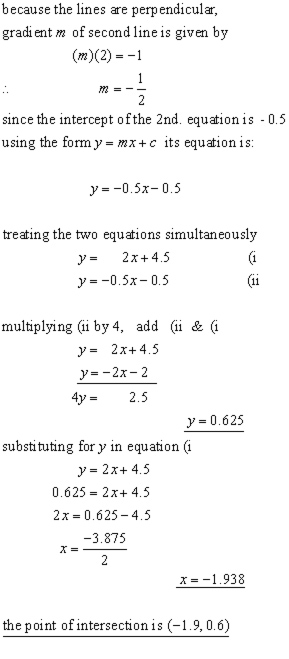
Finding the Equation of a Straight Line from One Point and the Gradient

Solution is by using the expression for gradient(m) for an actual point(x₁,y₁) and a generalized point(x,y).

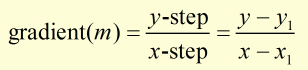
The straight line equation is found by substituting values of x₁, y₁ and m into the above.

Example

A line of gradient 3 passes through a point (2,5). What is the equation of the line?

back to top

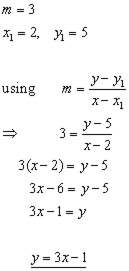
Finding the Equation of a Straight Line from Two Points

Solution is by first finding the gradient m from the x and y values from the points (x₁,y₁) and (x₂,y₂)

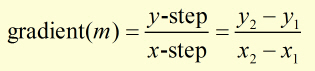
The straight line equation is found by substituting for x₁, y₁ and m into the equation for one point and the gradient(previous to the above equation).

Example

Find the equation of the line between the two points (2,3) and (-5,7).

back to top

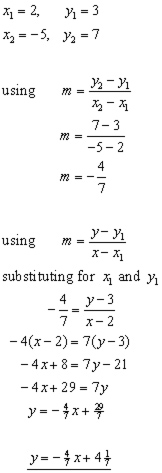
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]