Home >>STATISTICS, Section 1, correlation
first principles |
Correlation
Correlation is simply the relationship between one set of data and the other.
It is expressed as a number called the correlation coefficient(r) and has a range of values between -1 and +1 .
There are a number of different correlation coefficients derived from different statistical principles. Here are a few of the more important ones:
Product Moment correlation coefficient ( rpm)
Spearman's Rank correlation coefficient ( rS)
We shall deal with only the Product Moment* Correlation Coefficient here in Section 1.
Spearman's Rank Correlation is dealt with in the last section - Section 3.
*sometimes called Pearson's Product Moment
Product Moment Correlation Coefficient (rpm)
By definition, the Product Moment Correlation Coefficient is the covariance of two variables divided by the product of their standard deviations.
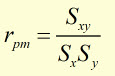
The more familiar form is:
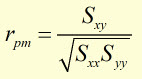
where,
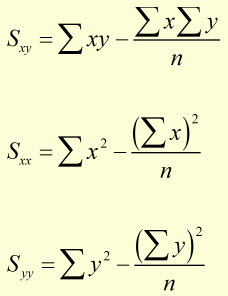
Properties
Product moment correlation coefficient has no units.
It is symmetric. The coefficient for x versus y is the same as for y versus x.
It is independent of change in origin and scale.
Example
The table describes the % exam results of 10 students taking Physics and French.
Calculate the Product Moment correlation coefficient and comment on the result.
physics |
45 |
76 |
71 |
68 |
54 |
59 |
74 |
60 |
48 |
43 |
French |
57 |
84 |
69 |
72 |
83 |
65 |
75 |
72 |
56 |
38 |
The first step is to make a table to calculate x2 , y2 and xy.
physics(x) |
French(y) |
x2 |
y2 |
xy |
45 |
57 |
2,025 |
3,249 |
2,565 |
76 |
84 |
5,776 |
7,056 |
6,384 |
71 |
69 |
5,041 |
4,761 |
4,899 |
68 |
72 |
4,624 |
5,184 |
4,896 |
54 |
83 |
2,916 |
6,889 |
4,482 |
59 |
65 |
3,481 |
4,225 |
3,835 |
74 |
75 |
5,476 |
5,625 |
5,550 |
60 |
72 |
3,600 |
5,184 |
4,320 |
48 |
56 |
2,304 |
3,136 |
2,688 |
43 |
38 |
1,849 |
1,444 |
1,634 |
598 |
671 |
37,092 |
46,753 |
41,253 |
(Σx) |
(Σy) |
(Σx2) |
(Σy2) |
(Σxy) |
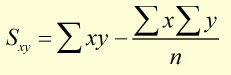
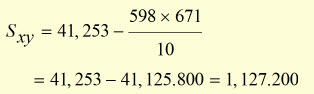 |
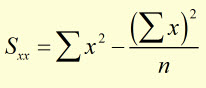
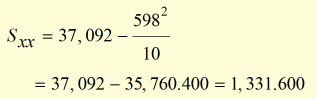 |
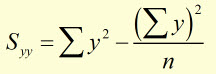
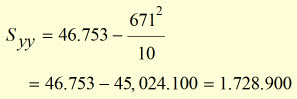 |
remembering that,
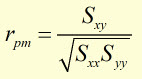
substituting for Sxy Sxx and Syy
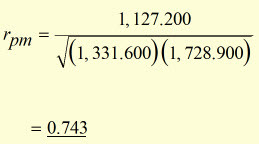
From the table of relationship strengths, a rpm of 0.743 means that there is a strong relation between performance in physics and French.
Students do equally well in both.
rpm |
relationship |
|---|---|
| -1.0 to –0.5 or 1.0 to 0.5 | Strong |
| -0.5 to –0.3 or 0.3 to 0.5 | Moderate |
| -0.3 to –0.1 or 0.1 to 0.3 | Weak |
| –0.1 to 0.1 | None or very weak |
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
