Home >> PURE MATHS, Differential Calculus, the derivative formula

First Principles

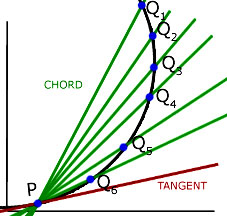
To find an expression for the gradient of the tangent at point P on a curve, we must consider lines passing through P and cutting the curve at points Q₁ Q₂ Q₃ Q₄ Q₅ Q₆ ...etc.

As Q approaches P so the gradient of the chord PQ approaches the gradient of the tangent at P.

We can form an expression for the gradient at P by using this concept.

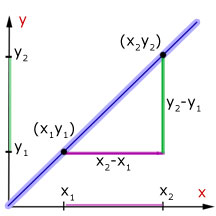
We know from coordinate geometry that:

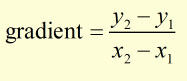
for points (x₁y₁) and (x₂y₂)

Consider the coordinates of P to be (x,y) and point Q to be (x+dx, y+dy), where dx and dy are the horizontal and vertical components of the line PQ.

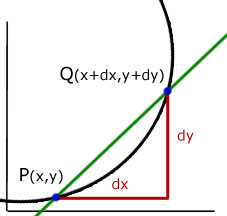
Gradient of the line between points (x,y) and (x+dx, y+dy) is given by :

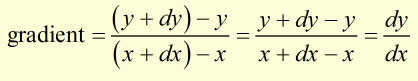
The tangent to the curve = gradient of PQ when the length of PQ is zero and dx = 0 and dy = 0.

In the limit, as dx 'approaches zero' the gradient of the curve is said to be dy/dx.

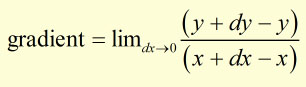
Since,

if we incrementally increase both y and x , then

Now we can substitute for y + dy in the top bracket of the 'gradient' equation.

At the same time we can replace the y by f(x) .

In the bottom brackets the +x and the -x cancel out, leaving dx

Then we have:

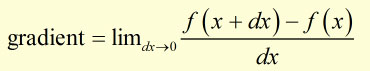
that is,

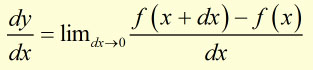
Example: Find the gradient of   y = 4x².

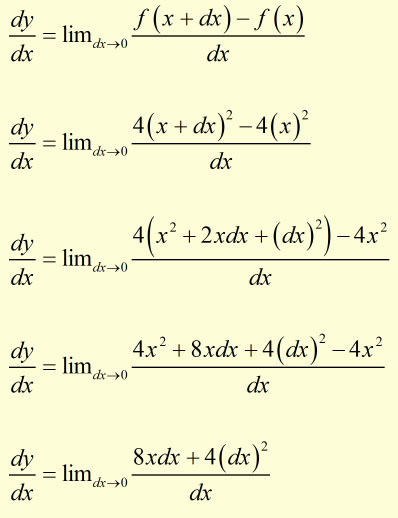
cancelling by dx,

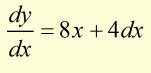
in the limit when dx = 0 this becomes,

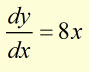
Without doubt this is a very long winded way to work out gradients. There is a simpler way, by using the Derivative Formula.

back to top

Notation This is best described with an example.

If  y = 3x² , which can also be expressed as f(x)= 3x², thenthe derivative of y with respect to x can be expressed as:

back to top

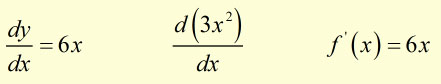
The Derivation Formula

If we have a function of the type  y = k x ⁿ , where k is a

constant, then,

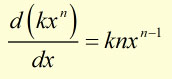
example #1

Find the gradient to the curve  y = 5 x² at the point (2,1).

gradient = (5) (2 x^2-1) = 10 x¹ = 10 x

gradient at point (2,1) is 10 x 2 = 20

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]