Home >> PURE MATHS, Algebra, laws of logarithms
laws |
The Laws of Logarithms
![]()
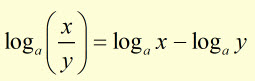
![]()
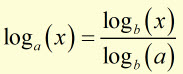
![]()
![]()
Proofs #1
prove that 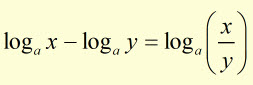
let ![]() (i
(i
![]() (ii
(ii
then ![]()
![]()
it follows that 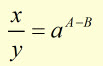
taking logs to the base 'a' each side,
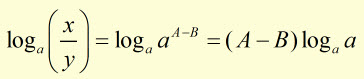
but ![]()
therefore 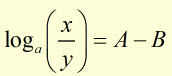
substituting for A and B from (i and (ii
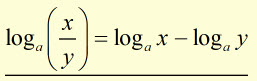
Proofs #2
prove that 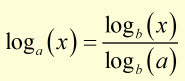
let ![]()
which implies that ![]()
taking logs on both side to the base 'b'
![]()
![]()
rearranging to make 'y' the subject
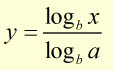
substituting for 'y' ( ![]() )
)
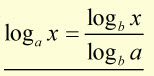
Changing the Base
Remember that the change of base occurs in the term where the base is 'x' or some other variable.
Example #1
solve for x ![]()
changing ![]() to the base '2'
to the base '2'
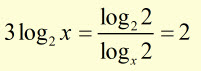
multiplying both sides by ![]()
![]()
rearranging ![]()
remembering that ![]()
![]()
factorising the quadratic
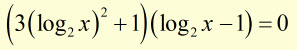
giving roots
![]()
![]()
![]() (implying that)
(implying that)
![]()
![]()
![]()
Simultaneous Equations
'Substitution' simultaneous equations are common problems.
method:
| 1. first find what x is in terms of y |
| 2. then substitute for x in the other equation |
| 3. solve for y |
Example #1
given that ![]() (i
(i
and ![]() (ii
(ii
find x and y
![]()
implies that ![]()
but ![]()
![]()
![]()
![]() (iii
(iii
substituting for x into (ii
![]()
![]()
![]()
![]()
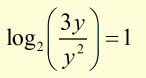
![]() (implying that)
(implying that)
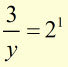
![]()
answer ![]()
![]()
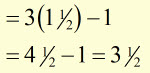
answer ![]()
Variable in the Index
method:
1. take logs on both sides |
2. move the indices infront of the logs |
3. expand the equation |
4. collect x-terms to the left |
| 5. sum the numbers to the right |
These problems can be tricky with the amount of arithmetic involved.
So make sure you write everything down to make checking your working easier.
Example #1
solve for x to 3 d.p. ![]()
taking logs to base 10 on each side
![]()
expanding the powers
![]()
substituting the values of logs to base 10 for 2, 3 and 6
![]()
expanding,
![]()
collecting terms,
![]()
![]()
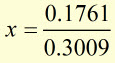
![]()
![]() to 3 d.p.
to 3 d.p.
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
