Home >> PURE MATHS, Algebra, number set theory

Introduction

A set is a collection of objects, numbers or characters.

{abcdef....wxyz}  {1,2,3,4,...45, 46, 47}   etc.

Note how the set is enclosed in brackets {.....}

A definite set is one in which all its members are known.

Sets are given uppercase letters: A, B, C, etc.

The elements of sets are given lowercase letters: a, b, c,..etc.

An element x belonging to the set A is written:

A constraint bar {...|...} is for setting a property that all members satisfy.

e.g. A{x l x has the colour blue} - all elements of A are blue

back to top

Common Sets

back to top

Venn Diagrams

Venn Diagrams are used to visualise sets and their relations to one another.

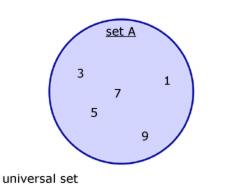
Above is a diagramatic representation of set A.

The set can be represented mathematically as: A{1,3,5,7,9} .

Note that set A(the circle) is a subset of the Universal set(the rectangle).

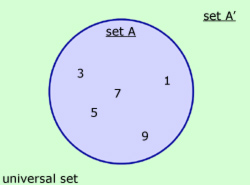
A' (A-dash)is called the complement of A.

It contains all elements that are not members of A.

A and A' together make up the Universal set.

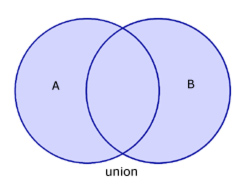
The union of sets A and B contains all of the elements from both sets.

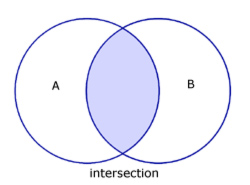
The intersection of sets A and B contains a particular group of elements that exist in set A and in set B.

back to top

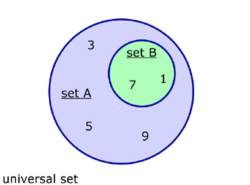
Subsets

If B is a subset of A. Then all of the elements of B are also in A.

back to top

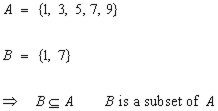
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]