Home >> PURE MATHS, Vectors, general properties

Notation

A non-zero vector has the magnitude of a positive real number and a direction in space.

Representation is by two letters describing a line.

The order of the letters indicates the direction and the length of the line its magnitude.

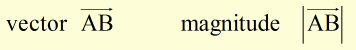
An alternative to this notation is to use a single bold letter, for example C.

Then the magnitude is |C| or C.

back to top

The Unit Vector

A unit vector eg a, has a magnitude of one |a|=1 and can point in any direction.

A unit vector is usually written with a circumflex accent over it    â.

Examples: 1 Newton, 1 ms^-1 , 1 metre etc.

Hence, if A is an ordinary vector,

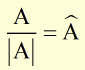
Â('A' hat) is a unit vector in the direction of A.

back to top

2D Representation

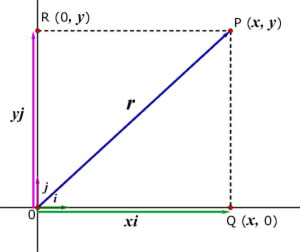
P is a point in the x-y plane with coodinates (x,y).

i is the unit vector along the x-axis.

j is the unit vector along the y-axis.

With Q at (x,0) and R at (0, y):

back to top

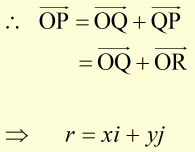
3D Representation

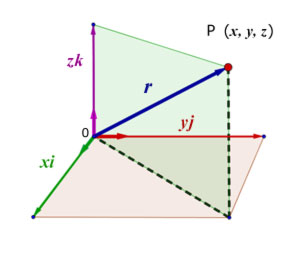
P is a point in x-y-z space with coodinates (x, y, z).

i is the unit vector along the x-axis.

j is the unit vector along the y-axis.

z is the unit vector along the z-axis.

back to top

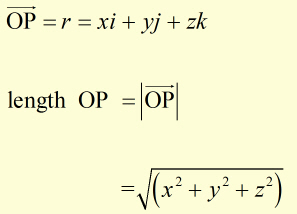
Addition(Sum) of Vectors

This is also called the Parallelogram or Triangle Law.

If two vectors(a & b) are represented in magnitude and direction by the adjacent sides of a parallelogram from a point, then their resultant(r) is represented in magnitude and direction by the diagonal of the parallelogram passing through the point.

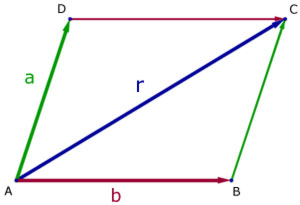
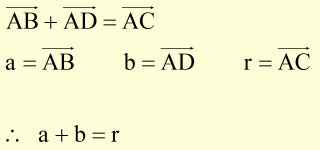
If two vectors are represented in magnitude and direction by the adjacent sides of a triangle, taken in order, then their resultant is represented in magnitude but opposite in direction by the third side.

back to top

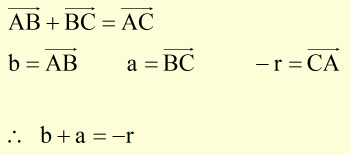
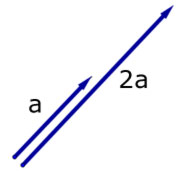
Scalar Multiplication

Multiplying a vector by a scalar quantity changes its magnitude but not its direction.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]