Home >> PURE MATHS, Differential Calculus, maximuma & minima

Gradient Change

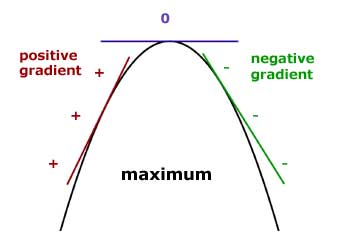
Starting to the left of a maximum the gradient changes from     ' + ' to ' - 'with increasing 'x'.

Starting to the left of a minimum, the gradient changes from     ' - ' to ' + 'with increasing 'x'.

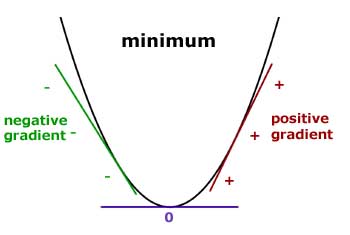
At the point of maximum or minimum the gradient is zero.

Example    Show that the curve y = x² has a minimum at (0,0).

back to top

Locating the point of maximum or minimum

The x-value at a maximum or minimum is found by differentiating the function and putting it equal to zero.

The y-value is then found by substituting the 'x' into the original equation.

Example   

Find the coordinates of the greatest or least value of the function:

back to top

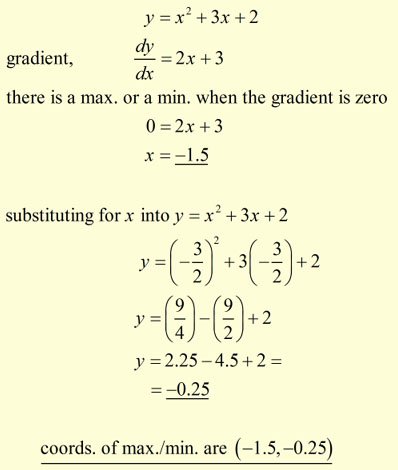
Curve Sketching

The power of 'x' gives a hint to the general shape of a curve.

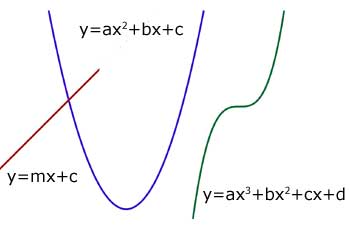
Together with the point of maximum or minimum, where the curve crosses the axes at y=0 and x=0 gives further points.

Example

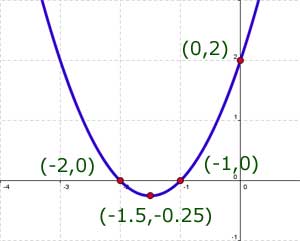
Sketch the curve y = x² +3x +2 from the example above, given that there is a minimum point at (-1.5,-0.25).

Factorising and putting y=0 to find where the curve crosses the x-axis,

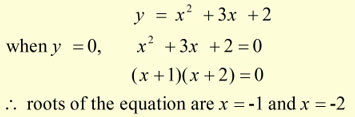
So the curve crosses the x-axis at (-1,0) and (-2,0).

Putting x=0 to find where the curve crosses the y-axis we find that y=2.

So the curve crosses the y-axis at (0,2).

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]