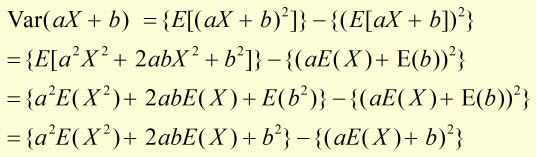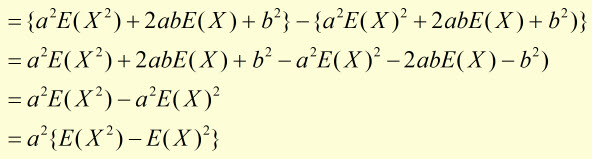Home >>STATISTICS, Section 1, discrete random variables 3

Variance of a discrete random variable Var(X)

By definition,

variance is a measure of the spread(dispersion) of a set of data points around their mean value.

Mathematically, the variance is the expectation( mean) of the averageof the squared deviations from the mean.

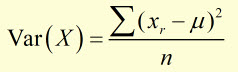
where,

x_r is any value of the random variable x
μ is the mean value of x
n is the number of values of x
Σ means the sum of all values in the brackets

back to top

Variance and Expected Values

Variance can also be written in terms of the expectation operator E( ) :

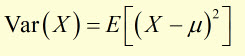
This can be expanded and consolidated to another form:

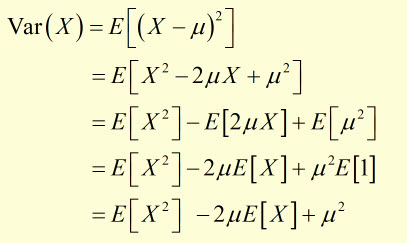
Substituting for E[X] from μ = E[X] :

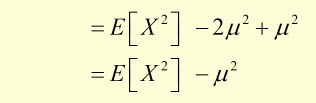
or

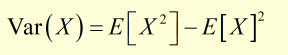
So the mean μ , the variance Var(X) and the standard deviation σ (sigma) are all related to one another.

back to top

Variance and Linearity

In a similar way to the Expectation Operator for E[aX + b] , the Variance Operator Var( ) behaves in a similar, though not identical, fashion.

However,                

This can be derived from first principles.

Using,  

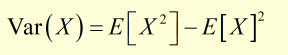
(from above)

and replacing X with aX+b,

since,                          

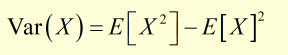
then,                    

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]