Home >> PURE MATHS, Integration, integration 'by substitution'

The Substitution Method(or 'changing the variable')

This is best explained with an example:

Like the Chain Rule simply make one part of the function equal to a variable eg u,v, t etc.

let    

Differentiate the equation with respect to the chosen variable.

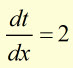
Rearrange the substitution equation to make 'dx' the subject.

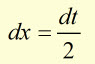
Substitute for 'dx' into the original expression.

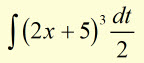
Substitute the chosen variable into the original function.

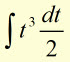
Integrate with respect to the chosen variable.

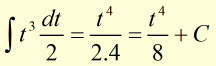
Restate the original expression and substitute for t.

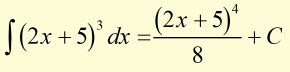
NB Don't forget to add the Constant of Integration (C) at the end.

     Remember this is an indefinite integral.

back to top

Example #1

make  

then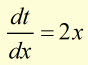    

rearranging,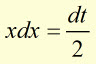                

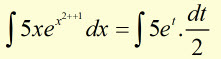
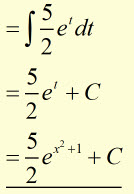
back to top

Example #2

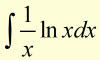
make  

then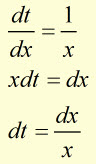  

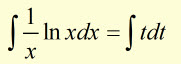
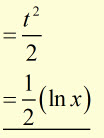
back to top

Example #3

let  

then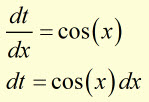  

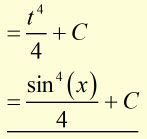
back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]