Home >> PURE MATHS, Algebra, the binomial theorem

Introduction

This section of work is to do with the expansion of (a+b)ⁿ and (1+x)ⁿ .

Pascal's Triangle and the Binomial Theorem give us a way of expressing the expansion as a sum of ordered terms.

Pascal's Triangle

This is a method of predicting the coefficients of the binomial series.

Coefficients are the constants(1, 2, 3, 4, 5, 6 etc.) that multiply each variable, or group of variables.

Consider (a+b)ⁿ variables a, b .

The 1st. line represents the coefficients for n=0.

(a+b)⁰= 1

The 2nd, line represents the coefficients for n=1.

(a+b)¹= a + b

The 3rd. line represents the coefficients for n=2.

(a+b)²= a² + 2ab + b²

Hence for the 6th. line . . .

The 6th. line represents the coefficients for n=5.

(a+b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

The Binomial Theorem builds on Pascal's Triangle in practical terms, since writing out triangles of numbers has its limits.

back to top

The General Binomial Expansion ( n ≥ 1 )

This is a way of finding all the terms of the series, the coefficients and the powers of the variables.

The coefficients, represented by ⁿC_r , are calculated using probability theory.

For a deeper understanding you may wish to look at where ⁿC_r comes from; but for now you must accept that:

where,

'n' is the power/index of the original expression

'r' is the number order of the term minus one

If n is a positive integer, then:

Example #1

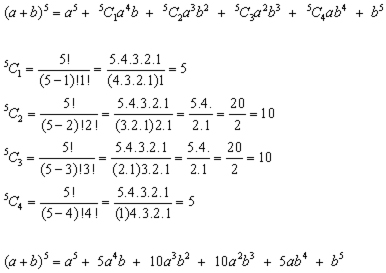
Example #2

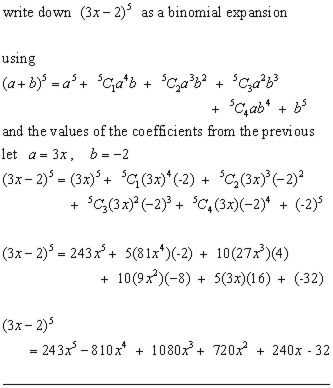
It is suggested that the reader try making similar questions, working through the calculations and checking the answer here (max. value of n=8)

back to top

The Particular Binomial Expansion

This is for (1+x)ⁿ ,

where,

n can take any value (positive or negative)

x is a fraction in the range -1 < x < 1

Example

Find the first 4 terms of the expression (x+3)^1/2 .

back to top

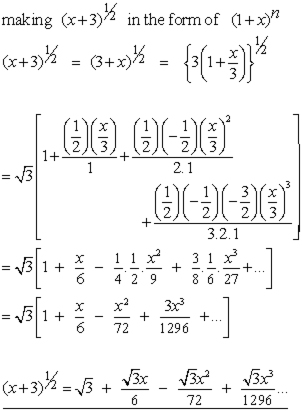
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]