Home >> PURE MATHS, Vectors, the scalar product

Introduction

The Scalar Product (or Dot Product), of two vectors a and b is written

If the two vectors are inclined to each other by an angle(say θ ) then the product is written:

a.b = |a|.|b|cosθ      or     a.b = abcosθ

Even though the left hand side of the equation is written in terms of vectors, the answer is a scalar quantity.

Rules

a.b = abcos θ = b.a

When a & b are parallel, θ = 0,   cos θ = 1 , a.b = ab .

(unit vectors i.i = j.j = k.k = 1)

When a & b are at 90^o , θ = 90^o,   cos θ = 0 , a.b = 0 .

(unit vectors:    i.j = j.i = 0    j.k = k.j = 0     k.i = i.k = 0)

If    a = a₁i + a₂j + a₃k    and    b = b₁i + b₂j + b₃k

then,

a.b = a₁b₁ + a₂b₂ + a₃b₃

|a|² = a.a = a₁² + a₂² + a₃²

a.(b + c) = a.b + a.c

a.(b - c) = a.b - a.c

(a + b).c = a.c + b.c  

(a - b).c = a.c - b.c

(λa).b = λ(a.b) = a.(λb)      Where λ is a scalar constant.

back to top

Example #1

Given that,

a = 3i - j + 2k   and   b = 2i + j - 2k ,

find a.b and the included angle between the vectors to 1 d.p.

back to top

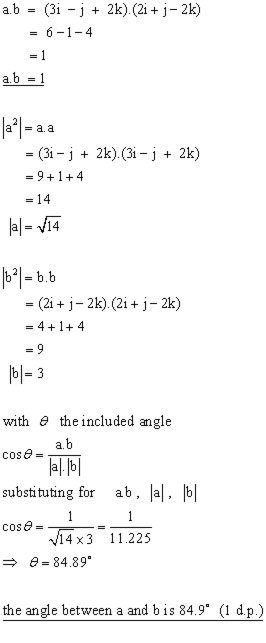
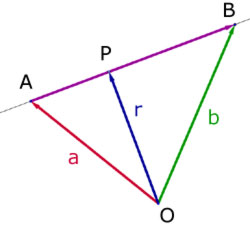
Example #2

i) What is the vector equation describing the straight line passing through the points A(-8, 1, -2) and B(10, -1, 3)?

ii) Find the coordinates of a point P on AB such that OP is perpendicular to AB(origin O), hence find the distance OP to 2 d.p.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]