Home >>STATISTICS, Section 1, discrete random variables 4

Revision

A continuous random variable can have any value between two specified values.

eg   x = 3.14   from   2 < x < 4

A discrete random variable has only one value chosen from a list of exact values.

eg   x = 7    from  3, 4, 5, 6, 7, 8, 9

Definition of a Discrete Uniform Distribution

This is a probability distribution where a number of equally spaced values are equally likely to happen.

If there are  n values each has an equal probability 1/n of occuring.

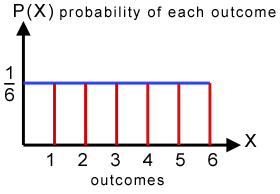
Take the example of throwing a fair die. The graph below describes the distribution of probabilities.

The appearance is a straight line. Each probability for each event is the same.

In mathematical terms, a discrete normal distribution is a set of n integer values.

Values vary incrementally from the lowest value, a to the highest value, b.*

a,   a+1,   a+2,   a+3, .  .  .  . b-3,   b-2,   b-1,   b

*note a and b are both integers, where a < b

The number of values is b - a + 1 .

To make this clear, think of a series that starts with a = 3 and ends with b = 11 .

Since each value is incremented by '1' , the number of values is ( 11 - 3 + 1 = 9 )

3   4   5   6   7   8   9   10   11

So the probability P(X = x) of each value occuring 1/n , is given by:

back to top

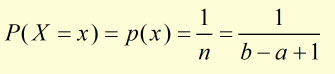
Derivation of Expected Value (for discrete uniform distribution)

Generally, the expected value is given by:

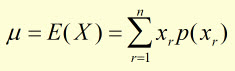
but p(x_r) is the same for each vale, that is 1/n , hence:

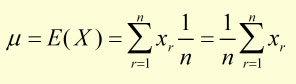
The expression is the sum(S) of an arithmetic progression, with the first term a ,

last term is b a common difference of '1' and n terms.

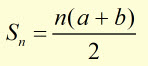
hence,

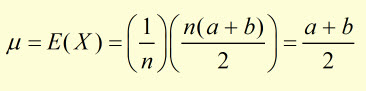
In the example of tossing a fair die*, a = 1 and b = n .

*or any situation where the outcomes are consecutive numbers starting with 1

back to top

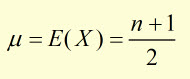
Derivation of Variance (for discrete uniform distribution)*

*simplified case with a = 1 and b = n

Variance is found from the expected value expression:

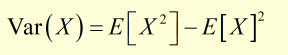
We already have E(X) from above. So E(X)² is given by:

E(X)² is found from:

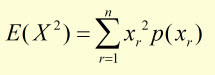
This simplifies to:

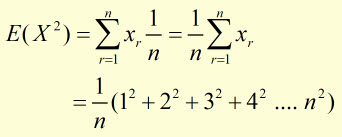
The sum S_n of a series of n squared numbers is given by:

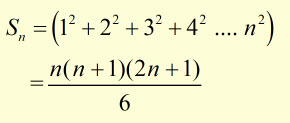
therefore,

cancelling the n's

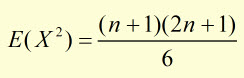
substituting for E(X²)and E(X)² into the Var(X) equation:

back to top

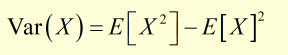
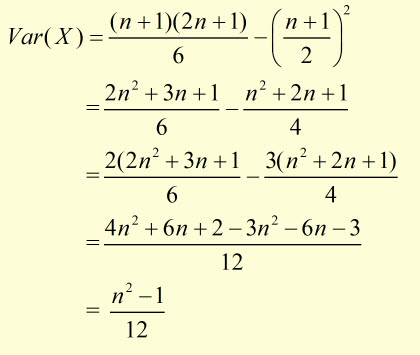
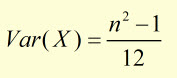
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]