Home >>STATISTICS, Section 1, discrete random variables 2
first principles |
The Mean μ (mu) Expected Value or Expectation of X E(X)
By definition, the mean μ of X is the weighted average of all the possible values of X .
Weighting is assigned according to the probability of the event happening.
The mean is the sum of :
(each possible outcome xr) x (each outcome probabilityP(xr)
for all values of x from r = 1 to r = n .
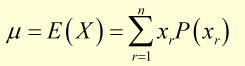
Example
Find the expected value when a fair die is rolled once, when the outcomes are:
1 2 3 4 5 6
Because there are 6 outcomes and each is equally possible, the probability of any one occurring is 1/6 .
Remembering that X represents the outcome being examined.
So the probability that a '4' is thrown is written:
P(X=4) = 1/6
Since all the probabilities are the same...
P(X=1) = P(X=2) = P(X=3) = P(X=4) = P(X=5) = P(X=6) = 1/6
The mean μ is the sum of :
(each possible outcome xr) x (each outcome probabilityP(xr)
for all values of x from r = 1 to r = n . In this case n = 6 .
|
μ = 1 x P(X=1) + 2 x P(X=2) + 3 x P(X=3)
+ 4 x P(X=4) + 5 x P(X=5) + 6 x P(X=6)
μ = (1 x 1/6) + (2 x 1/6) + (3 x 1/6)
+ (4 x 1/6) + (5 x 1/6) + (6 x 1/6) = 7/2 = 3.5 |
The answer 3.5 is exactly halfway between the die values of 1 and 6.
1 2 3 3.5 4 5 6
Mean(Expected Value) of a function of x E[ f(x) ]
The mean is given by the sum of:
(each possible outcome of the function f(xr) ) x (each outcome probabilityP( f(xr) )
for all values of x from r = 1 to r = n .
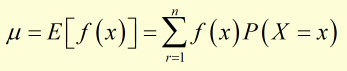
Example
Using a fair die, find the expected value(mean) of the cube of all outcomes.
f(x) = x3
μ = f(1) x P(X=1) + f(2) x P(X=2) + f(3) x P(X=3)
+ f(4) x P(X=4) + f(5) x P(X=5) +f(6) x P(X=6)
μ = (1) x P(X=1) + (8) x P(X=2) + (27) x P(X=3)
+ (64 x 1/6) + (125 x 1/6) +(216 x 1/6)
μ = (1 x 1/6) + (8 x 1/6) + (27 x 1/6)
+ (64 x 1/6) + (125 x 1/6) +(216 x 1/6)
μ = (1/6) + (8/6) + (27/6)
+ (64/6) + (125/6) +(216/6) = 441/6 = 73.5 |
1 8 27 64 73.5 125 216
Linearity of the expectation operator E( ) E[aX + b]
Where the function of x, f(x) is linear, it has the general form:
f(x) = aX + b
The expected value(mean) of a constant is a constant.
| E[a] = a (i |
The expected value(mean) of a random variable multiplied by a constant is the same as the constant multiplied by the mean of the random variable alone.
E[aX] = E[a] E[X]
Since E[a] = a , then:
E[aX] = aE[X] (ii |
(ii
So from (i & (ii above, if f(x) = aX + b
E[f(x)] = E[aX + b] = aE(X) + b
Example
A spinner has the shape of a regular pentagon. Sides are numbered 3, 5, 7, 7, 3 respectively.
i) What is the expected value E(X) for the outcomes?
ii) If each number on the spinner is increased by 2, what is the new expected value?
iii) If the original numbers on the spinner are increased by a factor of 2, what is the new expected value ?
i)
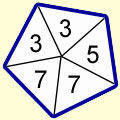
x |
3 |
5 |
7 |
P(X = x) |
2/5 |
1/5 |
2/5 |
E(X) = 3(2/5) + 5(1/5) + 7(2/5)
= 6/5 + 5/5 + 14/5
= 25/5 = 5
ii)
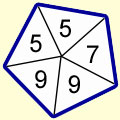
(3+2) |
(5+2) |
(7+2) |
|
x+2 |
5 |
7 |
9 |
P(X+2 = x+2) |
2/5 |
1/5 |
2/5 |
E(X+2) = E(X) + E(2)
= E(X) + 2
= 5 + 2 = 7
iii)
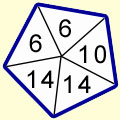
(2x3) |
(2x5) |
(2x7) |
|
2x |
6 |
10 |
14 |
P(2X = 2x) |
2/5 |
1/5 |
2/5 |
= 2 x 5 = 10
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
