Home >> PURE MATHS, Integration, the trapezium rule
Theory & Method |
Theory & Method
The Trapezium Rule is a method of finding the approximate value of an integral between two limits.
The area involved is divided up into a number of parallel strips of equal width.
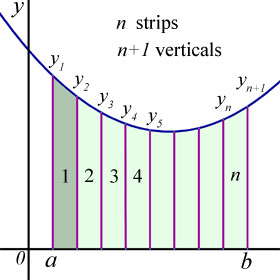
Each area is considered to be a trapezium(trapezoid).
If there are n vertical strips then there are n+1 vertical lines(ordinates) bounding them.
The limits of the integral are between a and b, and each vertical line has length y1 y2 y3... yn+1
width of each strip 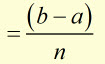
area of first strip = (width of strip) x (av. length of 1st. and 2nd. verticals)
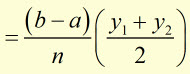
Therefore in terms of the all the vertical strips, while the actual integral is given by:
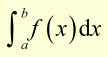
the approx. integral is
= (strip width) x [(av. of 1st. and last y-values) + (the sum of all y values between the second and second-last value)]
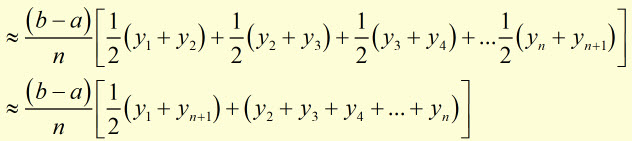
Example #1
using a strip width of ![]()
evaluate 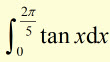
(answer to 2 d.p.)
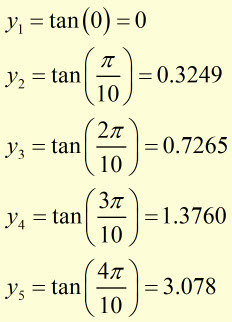
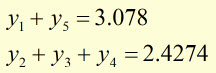
using approx. integral= (strip width) x [(av. of 1st. and last y-values)
+ (the sum of all y values between the second and second-last value)]
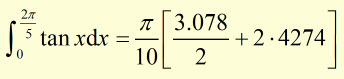
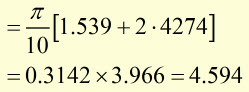
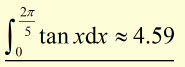
Example #2
using a strip width of '1' unit
evaluate 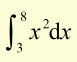
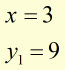
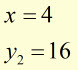
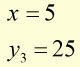
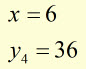
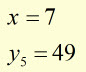
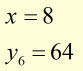
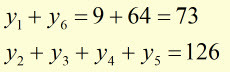
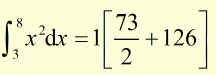
![]()
![]()
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
