Home >> PURE MATHS, Differential Calculus, differential equations

Definition

An equation containing any differential coefficients (shown below) is called a differential equation.

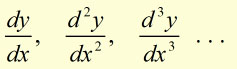
The solution of a differential equation is an equation relating x and y and containing no differential coefficients.

General & Particular Solution

The General Solution includes some unknown constant in the solution of a differential equation.

When some data is given, say the coordinates of a point, then a Particular Solution can be formed.

In this example the difference between the two solutions is self evident.

Example #1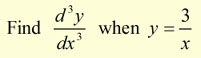    

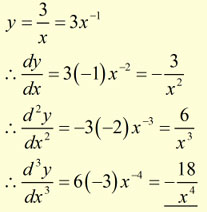
back to top

Example #2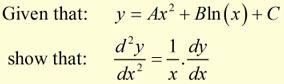      

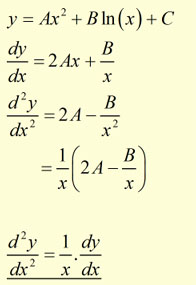
back to top

Points of Inflection(Inflexion)

The value of the second derivative can give an indication whether at a point a function has a maximum, minimum or an inflection.

These are all called stationary points.

A point of inflection has a zero gradient, where the point is not a maximum or a minimum value.

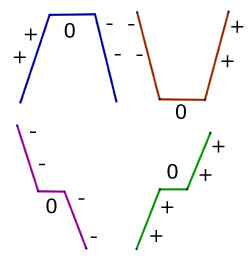
The point is where the gradient of a curve decreases(or increases) to zero before increasing(or decreasing) again.

Example

Find the stationary points of the function:

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]