Home >>STATISTICS, Section 2, binomial distribution 3

Cumulative Probability Tables - case of p<0.5

These give the tabulated value of P(X< x) .

This means that the probability displayed is less than or equal to an observed value of x.

The random variable X is distributed Binomially, where there are n trials and probability of success p .

Before going into any detail about using the tables, we must first look at their structure.
There are a number of table designs, but they more or less contain the same data. It is just a matter of emphasis.

The tables we are using were issued by the Edexcel Examinining Board(2009).

A binomial distribution X ~ B(n, p) has values of p (across the top)and n (down the left side) in the following ranges:

You can download a PDF copy of these tables, other tables and information on equations for A-level mathematics from the link below.

Mathematical Formulae Statistical Tables

(to download right click - "save target as" )

back to top

Case    P(X<x)

This is a straight forward lookup of the table.

Say that the random variable X has values X = 0, 1, 2, 3, 4, 5 ,

also that the probability of success p=0.35 and the number of trials n=6 .

We want to know the value of the probability that X is less than or equal to 3 . That is, the value of : P(X<3)

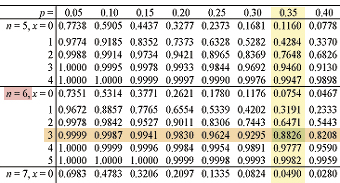
From the table:           P(X<3) = 0.8826

back to top

The case      P(X=x)

Using the values of n and p from before, let's say that we want to know the value of the probability that X is equal to 3. That is, the value of : P(X=3)

To understand this we must break down the values P(X<3) and P(X<2) into their constituent probabilities.

The probability that the random variable X is less than 3 or equal to 3 means that it can have values of '3' or '2' or '1' or '0'.

This can be written as the sum of probabilities. Remember for probability work, the operator '+' means OR .

P(X<3) = P(X=3) + P(X=2) + P(X=1) + P(X=0)

By the same reasoning,

P(X<2) = P(X=2) + P(X=1) + P(X=0)

subtracting the second equation from the first,

P(X<3) - P(X<2) = P(X=3)

turning the equation around,

P(X=3) = P(X<3) - P(X<2)

If we now look up the values for x = 3 and x = 2 from the tables:

P(X=3) = 0.8826 - 0.647  = 0.2355

back to top

The case     P(X<x)

Using the values of n and p from before, let's say that we want to know the value of the probability that X is less than 3. That is, the value of : P(X<3)

The probability that the random variable X is less than 3 means that it can have values of '2' or '1' or '0'.

This can be written as the sum of probabilities. Remember for probability work, the operator '+' means OR .

P(X<3) = P(X=2) + P(X=1) + P(X=0)

but,

P(X<2) = P(X=2) + P(X=1) + P(X=0)

therefore,

P(X<3) = P(X<2)

since   P(X<2) = 0.6471

P(X<3) = 0.6471

back to top

The case     P(X>x)

Using the values of n and p from before, let's say that we want to know the value of the probability that X is greater than 3. That is, the value of : P(X>3)

The probability that the random variable X is greater than 3 means that it can have values of '4' or '5' *

* the random variable X has values X = 0, 1, 2, 3, 4, 5

This can be written as the sum of probabilities. Remember for probability work, the operator '+' means OR .

P(X>3) = P(X=4) + P(X=5)

but the sum of all the individual probabilities equals '1' .

P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) = 1

rearranging, making P(X=4) + P(X=5) the subject,

P(X=4) + P(X=5) = 1 - [ P(X=0) + P(X=1) + P(X=2) + P(X=3)]

but,

P(X<3) = P(X=0) + P(X=1) + P(X=2) + P(X=3)

therefore,

P(X=4) + P(X=5) = 1 - P(X<3)

hence,

P(X>3) = 1 - P(X<3)

from the table,

P(X<3) = 0.8826

therefore,

P(X>3) = 1 - 0.8826 = 0.1174

back to top

The case     P(X>x)

Using the values of n and p from before, let's say that we want to know the value of the probability that X is greater than or equal to 3. That is, the value of : P(X>3)

The probability that the random variable X is greater than or equal to 3 means that it can have values of '3' or '4' or '5' *

* the random variable X has values X = 0, 1, 2, 3, 4, 5

This can be written as the sum of probabilities. Remember for probability work, the operator '+' means OR .

P(X>3) = P(X=3) + P(X=4) + P(X=5)

but the sum of all the individual probabilities equals '1' .

P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) = 1

rearranging, making P(X=3) + P(X=4) + P(X=5) the subject,

P(X=3) + P(X=4) + P(X=5) = 1 - [P(X=0) + P(X=1) + P(X=2)]

but,

P(X>3) = P(X=3) + P(X=4) + P(X=5)

and,

P(X<2) = P(X=0) + P(X=1) + P(X=2)

it follows that ,

P(X>3) = 1 - P(X<2)

putting in values,

P(X>3) = 1 - 0.6471 = 0.3529

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]