Home >> MECHANICS, Kinetics, newton's laws

Newton's Laws of Motion

1. A body will remain at rest or travel at uniform linear velocity unless acted upon by an external force.

2. The rate of change of linear momentum is proportional to the applied force and acts in the same direction as the force.

3. The forces of two bodies on each other are equal and directed in opposite directions.

Definition of Momentum

Momentum(p) is a vector quantity equal in magnitude to the product of mass and velocity.

Note, mass(m) is a scalar quantity, while velocity(v) is a vector quantity.

p= mv

m (kg)    v(ms^-1)    p (kg. ms^-1)

(The letter 'P' in upper case is designated to represent pressure. )

Theory

If we consider a force F acting on a mass m with velocity v, the Second law may be represented by the proportionality:

back to top

The Newton N

As seen from the theory relating to the Second Law, to get rid of the constant of proportionality each quantity is made unity.

So we come to our definition of a Newton:

A force of 1 Newton applied to a 1 kg mass will give it an acceleration of 1 ms^-2.

back to top

Linear acceleration

Here the mass is either stationary and is accelerated by a force in a straight line or is initially moving at constant velocity before the force is applied.

Example #1

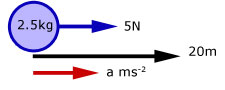
A 5N force acts on a 2.5kg mass, making it accelerate in a straight line.

i) What is the acceleration of the mass?
ii) How long will it take to move the mass through 20m?
(Answer to 2 d.p.)

i)

ii)

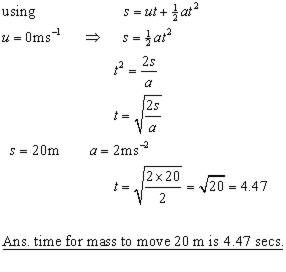
Example #2

A force causes a 3kg mass to accelerate. If the velocity of the mass at time t is given by:

v = 2ti - 3t²j + 4t³k

what is the magnitude of the force when t = 5 secs. ?

back to top

Linear retardation

Here the mass is already moving at constant velocity in a straight line before the force is applied, opposing the motion.

Example #1

A 4 kg mass travelling at constant velocity 15 ms^-1 has a 10 N force applied to it against the direction of motion.

i) What is the deceleration produced?
ii) How long will it take before the mass is brought to rest?

i)

ii)

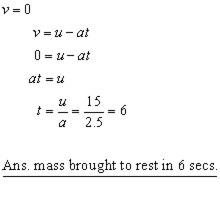
Example #2

A sky diver with mass 80kg is falling at a constant velocity of 70 ms^-1 . When he opens his parachute he experiences a constant deceleration of 3g for 2 seconds.

i) What is the magnitude of the decelerating force?
ii) What is his rate of descent at the end of the 2 seconds deceleration?

i)

ii)

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]