Home >> PURE MATHS, Coordinate Geometry, circles & ellipses

Circles

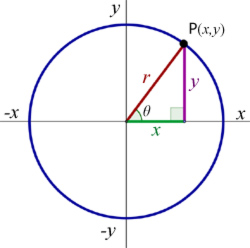
Any point P is described by Pythagoras' Theorem.

So the equation of a circle with centre (0,0)and radius r is given by:

or in terms of parameters,

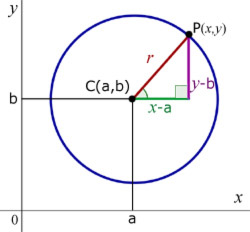
For a circle with its centre off-set from the origin at a point C(a,b), again, by Pythagoras, the equation is given by:

Circle equation expanded(usual form)

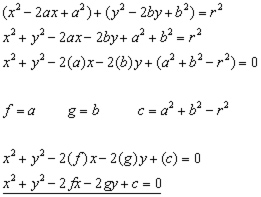
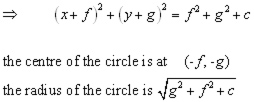
Example

What is the radius and the coodinates of the centre of the circle with equation:

back to top

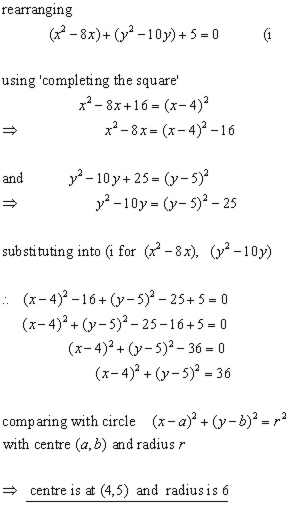
Ellipses

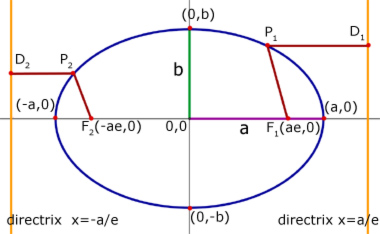
The maximum displacement (a) along the x-axis is called the semi-major axis.

The maximum displacement along the y-axis (b) is called the semi-minor axis.

The names apply when a>b. When b>a the names are interchanged.

The Eccentricity (e) of an ellipse is defined as:

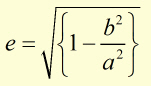
From the eccentricity we can define the points of focus (plural foci):

F₁ (ae,0) and F₂ (-ae,0)

and the directrices(directrix lines) at x = a/e , -a/e.

The directrices are two special lines parallel to the y-axis and either side of it.

(when the ellipse is centred at the origin)

Their unique property concerns the ratio of the distance between a point(P₁) on the curve to a focal point(F₁) and a line from the point to the directrix.

The ratio gives the eccentricity 'e' , where e < 1 :

back to top

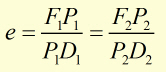
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]