Home >> PURE MATHS, Algebra, functions

Introduction

To thoroughly understand the terms and symbols used in this section it is advised that you visit 'Number Set Theory ' first.

Mapping(or function)

This a 'notation' for expressing a relation between two variables(say x and y).

Individual values of these variables are called elements .

eg   x₁ x₂ x₃...   y₁ y₂ y₃...

The first set of elements (x) is called the domain .

The second set of elements ( y) is called the range .

A simple relation like y = x² can be more accurately expressed using the following format:

The last part relates to the fact that x and y are elements of the set of real numbers R(any positive or negative number, whole or otherwise, INCLUDING zero).

back to top

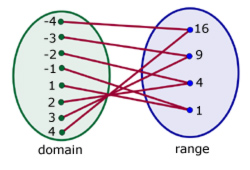
One-One Mapping

Here one element of the domain is associated with one and only one element of the range.

A property of one-one functions is that a on a graph a horizontal line will only cut the graph once.

Example

Where R⁺ is the set of positive real numbers.

back to top

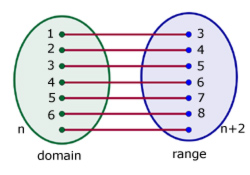
Many-One Mapping

Here more than one element of the domain can be associated with one particular element of the range.

Example

Where Z is the set of integers(positive & negative whole numbers NOT including zero).

Complete Function Notation is a variation on what has been used so far.

It will be used from now on.

back to top

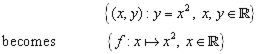
Inverse Function  f ^-1

The inverse function is obtained by interchanging x and y in the function equation and then rearranging to make y the subject.

If  f ^-1 exists then,

ff^-1(x) = f^-1f(x) = x

It is also a condition that the two functions be 'one to one'. That is that the domain of f is identical to the range of its inverse function  f ^-1 .

When graphed, the function and its inverse are reflections either side of the line   y = x.

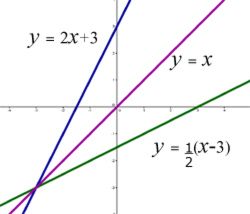
Example

Find the inverse of the function(below) and graph the function and its inverse on the same axes.

back to top

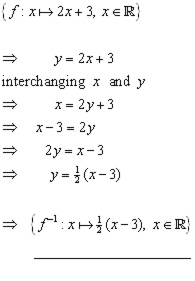
Composite Functions

A composite function is formed when two functions f, g are combined.

However it must be emphasized that the order in which the composite function is determined is important.

The method for finding composite functions is simply:

1. Find g(x).

2. Find f[g(x)].

Example

For the two functions,

find the composite functions    (i  fg   (ii  g f

back to top

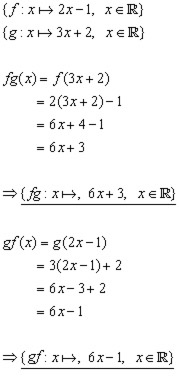
Exponential & Logarithmic Functions

Exponential functions have the general form:

where 'a' is a positive constant.

However there is a specific value of 'a' at (0,1) when the gradient is 1 .

This value, 2.718... or 'e' is called the exponential function.

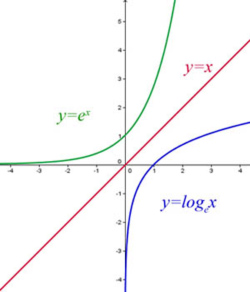
The function(above) has one-one mapping.

It therefore possesses an inverse. This inverse is the logarithmic function.

back to top

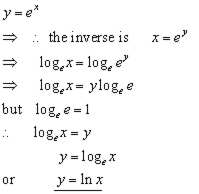
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]