Home >> PURE MATHS, Algebra, polynomials

Introduction

A polynomial is an expression which:

(where x a is variable, k is a constant and n a positive integer)

Every polynomial in one variable (eg 'x') is equivalent to a polynomial with the form:

Polynomials are often described by their degree of order.

This is the highest index of the variable in the expression.

(eg: containing x⁵ order 5, containing x⁷ order 7 etc.)

These are NOT polynomials:

3x²+x^1/2+x

The second term has an index which is not an integer(whole number).

5x^-2+2x^-3+x^-5

Indices of the variable contain integers which are not positive.

examples of polynomials:

x⁵+5x²+2x+3

(x⁷+4x²)(3x-2)

x+2x²-5x³+x⁴-2x⁵+7x⁶

back to top

Algebraic Long Division

If,

f(x) the numerator and d(x) the denominator are polynomials

and

the degree of d(x) <= the degree of f(x)

and

d(x) does not = 0

then,

two unique polynomials q(x) the quotient and r(x) the remainder exist.

So that:

Note - The degree of r(x) < the degree of d(x).

We say that d(x) divides evenly into f(x), when r(x)=0.

Example

back to top

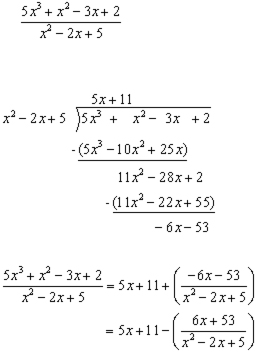
The Remainder Theorem

If a polynomial f(x) is divided by (x-a), the remainder is f(a).

Example

Find the remainder when (2x³+3x+x) is divided by (x+4).

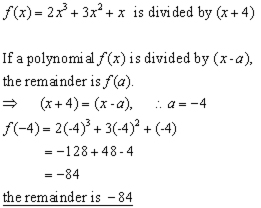
The reader may wish to verify this answer by using algebraic division.

back to top

The Factor Theorem (a special case of the Remainder Theorem)

(x−a) is a factor of the polynomial f(x) if f(a) = 0

Example

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]