Home >>STATISTICS, Section 1, probability 1

Basic Concepts

Probability(P) is a number falling within the limits 0≤ P ≤1 .

It is described as 'the chance of a particular outcome happening'.

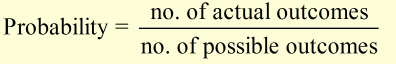
The probability of an event 'C' occuring when the outcome is certain (ie there is no other outcome) is 1.

This is written:

However, an event 'I' which is impossible has a probability of 0.

Similarly, this is written:

The probability of an event 'N' not happening is given by:

'N' not happening = 1 - (probability of it happening 'H')

In 'probability format' this is:

The sum of probabilities is always 1.

back to top

Set Notation

If the probability of one event X happening is P(X),

and

the probability of a different event Y happening is P(Y).

Then the probability of both events X AND Y happening is given by:

The probability of events X OR Y happening is given by:

The complement of an event is the probability of the event NOT HAPPENING.

This is written with an apostrophe after the 2nd bracket.

So the probability of event X not happening is written: P(X)' .

Adding the probabilities of the event happening and the event not happening gives 1.

This means that the event P(X) OR the event P(X)' will happen for certain.

Alternatively,

back to top

Venn Diagrams

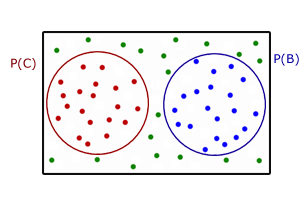
Say P(C) is the probability that students in a college choose chemistry.

So out of the whole college population N_totalonly a certain number N_chemistry (red dots) will make this choice.

The probability P(C) is given by:

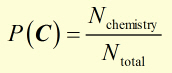
Likewise if students choose biology (blue dots), the probability P(B) of this is given by :

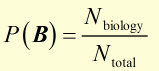
The total number of elements in a Venn diagram is represented by the sample space.

This is a rectangle. So all the students in the college( N_total) are contained within this space.

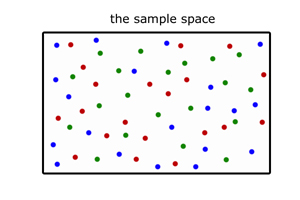
A Venn diagram is a way of ordering choices.

The probabilities P(C) and P(B) can be represented by circles within the rectangle, coralling the choices.

Now consider the case of students choosing both chemistry AND biology. This would be represented by an overlap of the two circles.

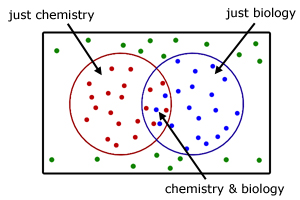
Then each group representing a choice of ' just chemistry' or 'just biology' would be the respective circles with a lens shaped area missing.

We can now write down an expression in set notation from the diagram.

  full blue circle + full red circle

=

 overlaps + (incomplete red circle + incomplete blue circle)

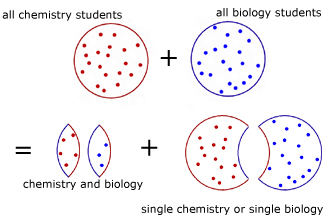
In words,

the probability of students choosing chemistry plus the probability of students choosing biology

=

the probability that students choose chemistry and biology plus the probability that students choose chemistry or biology

back to top

Example

Out of a group of 45 students, 17 are taking chemistry and 22 biology.

i) If 9 students do both chemistry and biology:

ii) What is the probability that of a student from the group is taking only the chemistry class? (ans, 3 d.p.)

Answer:

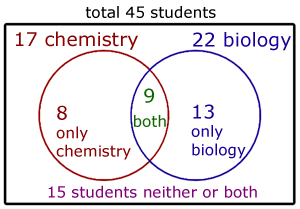
If only 9 students do chemistry & biology, then the number that do only chemistry,

   = (total no. chem. students) - (no. that do chem. & biology)

   = 17 - 9 = 8

Similarly, if 9 students do chemistry & biology, then the number that do only biology,

   = (total no. bio. students) - (no. that do chem. & biology)

   = 22 - 9 = 13

The no. of students doing single chemistry, single biology and both chemistry and biology

  = 8 + 13 + 9 = 30

Since the total no. of students is 45, those not taking any of these sciences = 45 - 30 = 15

To sum up,

i)

ii) The probability of studying only chemistry is,

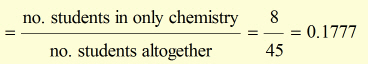
Final answer, to 3 decimal places, the probability is 0.178

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]