Home >>STATISTICS, Section 1, normal distribution 3

First Principles

More on z-tables

From z-tables the area under the curve of f(z) can be determined. z is read from the extreme left(- ∞) up to any positive value of z. This area Φ(z), is called the cumulative distribution function.

Hence when z = 0 the area is 0.5 . Note that the total area under the curve is 1.

If we want to measure the particular area(and hence cumulative probability) between discrete values we use a different form of the function: P(Z<z)

back to top

The case of P(Z<z)

So to evaluate P(Z<z) all we have to do is read off the value of Φ(z) for z from the tables.

Since in this case,

Φ(z) = P(Z<z)

Example

i) For a Standardized Normal Distribution N(0,1), evaluate the Cumulative Distribution Function(CDF) for the condition where z<1.9
ii) Sketch a curve to illustrate your answer.

i)

P(Z<1.9) = Φ(1.9) = 0.9713

ii)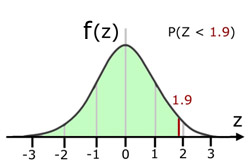                  

back to top

The case of P(Z>z)

(area under the curve to the right of any value z) =

(area under whole curve) - (area under curve up to value z)

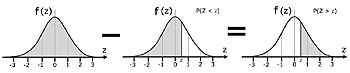
1  -  P(Z < z)  =   P(Z > z)

or

P(Z > z)  =   1  -   P(Z < z)

Example

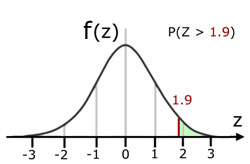
i) For a Standardized Normal Distribution N(0,1), evaluate the Cumulative Distribution Function(CDF) for the condition where z>1.9
ii) Sketch a curve to illustrate your answer.

i)

P(Z >1.9)  =   1  -   P(Z <1.9)

           =   1 -  0.9713

     =   0.0287

ii)

back to top

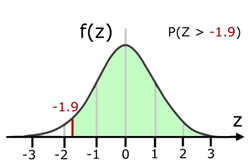
The case of P(Z>-z)

By symmetry,

(area under the curve to the left of a positive value of z) =

(area under the curve to the right of a negative value of z)

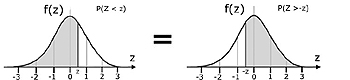
P(Z<z)  =  P(Z>-z)     

Example

i) For a Standardized Normal Distribution N(0,1), evaluate the Cumulative Distribution Function(CDF) for the condition where z>-1.9
ii) Sketch a curve to illustrate your answer.

i)

P(Z>-1.9) = P(Z<1.9)           

  P(Z<1.9) = Φ(1.9) = 0.9713

ii)

back to top

The case of P(Z<-z)

By symmetry,

(area under the curve to the left of a negative value of z) =

(area under the curve to the right of a positive value of z)

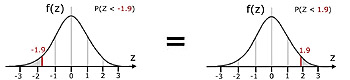
P(Z<-z)  =   P(Z>z)

from above,         P(Z>z)   =   1  -  P(Z < z)

therefore,            P(Z<-z)  =   1  -  P(Z < z)   

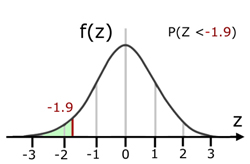
Example

i) For a Standardized Normal Distribution N(0,1), evaluate the Cumulative Distribution Function(CDF) for the condition where z<-1.9
ii) Sketch a curve to illustrate your answer.

i)

P(Z<-1.9)  =   1  -  P(Z <1.9)

                            =   1 - Φ(1.9) =    1 -  0.9713   = 0.0287

P(Z<-1.9) =   0.0287

ii)

back to top

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]