Home >>STATISTICS, Section 1, normal distribution 1

Introduction

An introduction to the Normal Distribution is given in Dispersion Part 3.

Here the concepts of variance,  standard deviation and their use for grouped data are introduced. The topics of  skewness and  outliers  are also touched upon.

The Normal Distribution

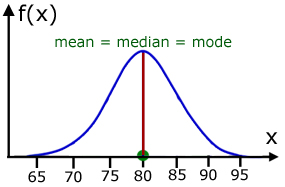
A Normal (or Gaussian) distribution is a symmetrical curve, with a central maximum.

The mean, mode and median all occur at one point along the x-axis, corresponding to the central maximum.

horizontal axis - continuous random variable    x.

vertical axis - probability density function of x    f(x) *

*this is also known as  density function, PDF or pdf.

properties of the curve:

i)  the graph of the density function is a continuous curve

ii) the area bounded by the curve and the x-axis = 1 (over the total continuous range of values( i.e. the variable's domain)

iii) probability of a random variable x  in the range a < x <  b is equal to the area under the probability density function curve bounded by a and b.

iv) the equation of the curve has the general form:

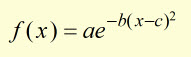
where,

i)   a and b are constants

ii)  the vertical line x = c is the axis of symmetry of the curve

iii) f(x) > 0 for all values of x

The basic equation can be expanded as:

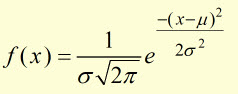
where,

back to top

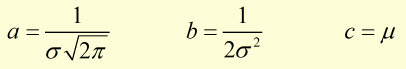
Standard Deviation and Probability

The area enclosed by the curve and discrete values is a measure of probability.

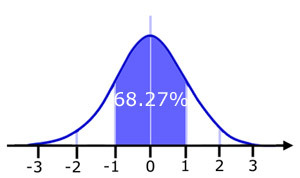
Approx. 68% of the values are within 1 standard deviation of the mean.

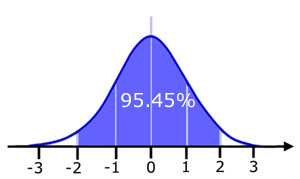
Approx. 95% of the values are within 2 standard deviations of the mean.

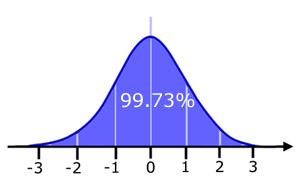
Approx. 99.7% of the values are within 3 standard deviations of the mean.

Summary

*either side of the mean

Example

68% of students score between 54% and 72% on their mathematics paper.

i) Assuming normally distributed data, give an approximate answer for the mean and standard deviation of the scores.

ii) using the results from part i), what is the range of scores obtained by 95% of the students?

i) mean =(72 + 54)/2 = 63%

68% is 1 standard deviation either side of the mean.

So 68% represents a total of 2 standard deviations.

1 standard deviation = (72 - 54)/2 = 9%

ii) 95% of the students is 2 standard deviations either side of the mean. That is 18% (2 x 9%) either side of 63%.

So the range of scores is:

63 -18 and 63 +18

45%  -  81%

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]