Home >> PURE MATHS, Integration, the integration formula

The Integration Formula or Power Rule

The expression to be integrated is the derivative of some function eg f(x) called the integrand.

When this expression is integrated the original function is restored plus a constant (C) called the constant of integration.

This is called the indefinite integral only when the integration is not between two limiting values of x.

However when the integration is between two limiting values of x then the integral is called the definite integral and the constant of integration is not involved.

For any variable 'x' to the power of 'n' the integral is given by:

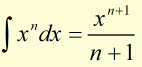
In other words, increase the power of x by '1' and divide x by the new index.

back to top

Some other integration Rules

The 'Constant' Rule

Any constant(eg C) multiplied by a function f(x) can be integrated by placing the constant before the integration sign.

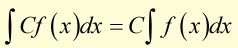
Example

back to top

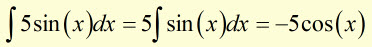
The 'Sum & Difference' Rules

The integral of two separate functions, that are added together, is the same as each function being integrated separately, then added together.

The integral of two separate functions, that are subtracted from one another, is the same as each function being integrated separately, and then subtracted as before.

Example

back to top

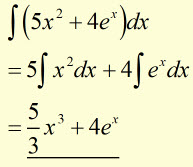
'Addition of a Constant' Rule

The addition of a constant to a variable doesn't change the form of the integral.

However, x must be in the first degree (ie no higher powers of x are involved).

if         then    

NB 'a' is a constant

Example

if 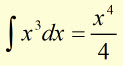        then    

back to top

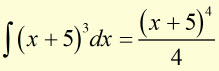
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]