Home >>STATISTICS, Section 2, binomial distribution 2

First Principles

Combinations   ⁿC_r

To appreciate the Binomial equation we must first have an understanding of combinations.

The definition of a Combination is:

'the number of ways r items can be chosen from a set of n items'

A short-hand way of writing this is ⁿC_r .

This can be written mathematically as:

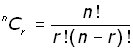
*note ! means 'factorial' - eg !3 = 3 x 2 x 1

Though an easier method of calculation, especially with large values of n, is to use a calculator.

Example

With 52 cards in a deck, how many ways can 3 different cards be chosen?

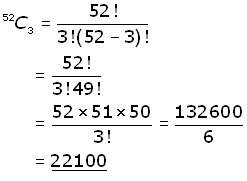
Using a calculator,

52   SHIFT    nCr   3    =    22100

back to top

The Binomial Equation

                  (i       

where the probability of failure,

Since,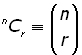                        

and           

the Binomial equation   (i   is sometimes expressed as:

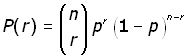
Example

Using the problem first given in Binomial distribution part 1 and extending it to probability prediction:

1 ball is chosen from a bag of 10 identical balls, each numbered (1-10). Once noted, the ball is returned to the bag.
A single ball is chosen on 3 separate occasions.
Success is in obtaining a '5' ball.

i) What is the probability of obtaining a single '5' ball in 3 choices?

ii) Draw a tree-diagram to find the probability of obtaining a single '5' ball in the last choice.

i)

let X be the random variable for obtaining a '5' ball.

X has possible values (0, 1, 2, 3).

The number of trials n = 3

The number of required successes r = 1

p probability of single successful trial (ie a '5' ball) = 1/10

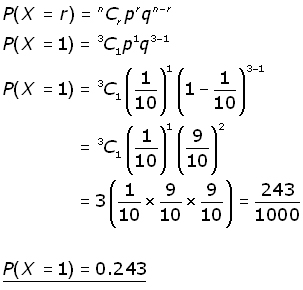
ii)

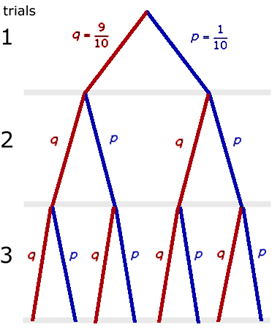
The probability(P) of getting a '5' ball with 3 tries is the sum of each of the probabilities for each successful attempt.

The sum sign '+' signifies an 'OR' decision.

The multiplication sign 'x' signifies the AND condition.

P = (q x q x p) + (q x p x q) + (p x q x q)

So the probability P_L of the last ball drawn being a '5' is given by:

P_L = (q x q x p) = (9/10) (9/10) (1/10) = 81/1000 = 0.081

back to top

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]